Autorem poniższego opracowania (wraz z rysunkami) jest dr Piotr A. Dybczyński z Instytutu Obserwatorium Astronomiczne UAM w Poznaniu.
Metoda eliminacji Gaussa
Mamy układ n równań z n niewiadomymi typu:
a11x1 + a12x2 + a13x3 + ... + a1nxn = b1
a21x1 + a22x2 + a23x3 + ... + a2nxn = b2
a31x1 + a32x2 + a33x3 + ... + a3nxn = b3
a41x1 + a42x2 + a43x3 + ... + a4nxn = b4
.
.
.
an1x1 + an2x2 + an3x3 + ... + annxn = bn
gdzie aij oznaczają współczynniki stojące przy j-tej niewiadomej w i-tym równaniu, natomiast bi oznacza "wyraz wolny" (lub "prawą stronę") i-tego równania, czyli liczbę po prawej stronie znaku równości, która nie jest mnożona przez żadną z niewiadomych.
Układ taki można zapisać w postaci macierzowej: Ax = B , przyjmując oznaczenia jak na Rys.1.
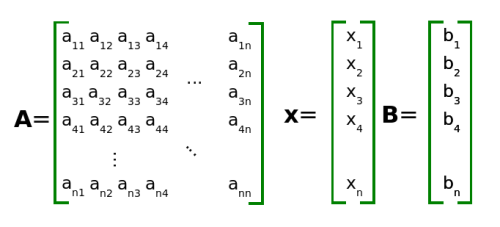
Rysunek 1.
Układ taki zapisuje się często przy pomocy jednej macierzy prostokątnej, powstałej przez dodanie do macierzy A dodatkowej kolumny "prawych stron", wziętej z wektora B.
Powstaje wtedy macierz prostokątna n na n+1 jak na Rysunku 2.
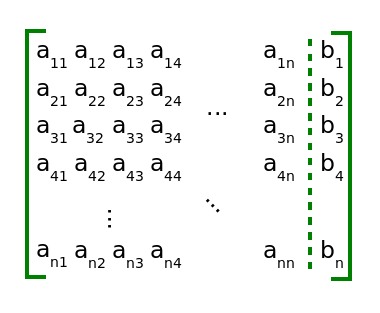
Rysunek 2.
Na przykład układ równań:
2 x1 - 2 x2 + 2 x3 - 7 x4 + 6 x5 = -4
7 x1 - 3 x2 - 2 x3 + 7 x4 + 2 x5 = 11
2 x1 + 2 x2 - x3 + x4 + 4 x5 = 9
9 x1 + 8 x2 - 2 x3 + 2 x4 - 2 x5 = 21
4 x1 + 8 x2 - 3 x3 + 3 x4 - x5 = 16
zapisujemy w postaci:
⌈ 2 -2 2 -7 6 -4 ⌉
| 7 -3 -2 7 2 11 |
| 2 2 -1 1 4 9 |
| 9 8 -2 2 -2 21 |
⌊ 4 8 -3 3 -1 16 ⌋
Gdyby ktoś próbował rozwiązywać ten układ, to prawidłowym rozwiązaniem jest: x1=1.0, x2=2.0, x3=3.0, x4=2.0, x5=1.0
Carl Friedrich Gauss
(Wikimedia Commons)
Metoda eliminacji Gaussa
Rysunek 3.
Rysunek 4.
Rozpoczynamy od pierwszego wiersza macierzy opisującej nasz układ równań (patrz Rys.3). Zakładając, że element a11 jest niezerowy (jeśli jest, to niezbędny będzie wybór elementu głównego, o którym niżej) dzielimy wszystkie elementy pierwszego wiersza (wraz z wyrazem wolnym) przez a11. W efekcie uzyskujemy wynik, jak na Rys.4.
Na przekątnej części kwadratowej (zamiast a11) pojawia się jedynka a pozostałe liczby z pierwszego wiersza, oznaczone tu jako w1j zmieniają wartość. Są to już elementy docelowej macierzy, zaznaczono je więc na czerwono. Zmieniła się też wartość w kolumnie wyrazów wolnych, oznaczona teraz jako z1. Wszystkie elementy pierwszego wiersza (te czerwone) nie zmienią już swojej wartości.
Rysunek 5.
Teraz, wykorzystując ten nowo otrzymany pierwszy wiersz będziemy "produkowali" zera w całej kolumnie poniżej jedynki. Aby uzyskać zero bezpośrednio pod jedynką (w drugim wierszu, pierwszej kolumnie) odejmujemy od całego drugiego wiersza wiersz pierwszy, pomnożony przez a21. W efekcie (patrz Rys.5.) pod jedynką pojawi się zero a pozostałe liczby w drugim wierszu (yxx i yx) zmienią swoje wartości. Nie będą to jednak wartości docelowe tylko wyniki pośrednie. Dopiero "produkowanie" jedynki zamiast elementu y22 przekształci wiersz drugi do postaci docelowej.
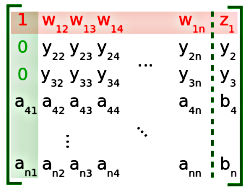
Rysunek 6.
Podobnie postępujemy z wierszem trzecim. Odejmujemy od niego pierwszy wiersz pomnożony przez a31, otrzymując wynik jak na Rys.6. Pojawia się kolejne zero w kolumnie pierwszej i kolejne tymczasowe współczynniki yij na pozostałych miejscach w wierszu trzecim.
Rysunek 7.
Dalej postępujemy tak samo z wierszem czwartym, piątym itd. aż do wiersza n-tego. W wyniku otrzymamy układ jak na Rysunku 7. Kolumna pierwsza składa się z jedynki na przekątnej (w miejscu elementu a11) i z samych zer w pozostałych wierszach. W ten sposób pierwszy wiersz i pierwsza kolumna otrzymały już postać docelową i w dalszych rachunkach nie będą już zmieniane. Zakończył się też pierwszy "krok" metody eliminacji Gaussa.
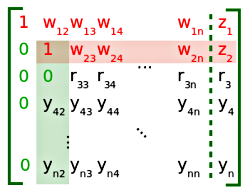
Rysunek 9.
Rysunek 8.
W następnym "kroku" przesuwamy się w dół i w prawo wzdłuż przekątnej, na miejsce elementu a22, który teraz ma wartość y22. Dzielimy cały wiersz przez y22 i "produkujemy" kolejną jedynkę na przekątnej oraz docelowe wartości współczynników wij w prawo od niej. Oczywiście optymalnie napisany program nie będzie dzielił elementów zerowych (w lewo od przekątnej), gdyż nie zmienia to ich wartości i jest zwykłym marnowaniem czasu. Wynik tej operacji widzimy na Rysunku 8. Dalej, jak w poprzednim "kroku", "produkujemy" zero w kolumnie drugiej wierszu trzecim, dzieląc ten wiersz przez wiersz drugi pomnożony przez y32. Wynik widać na Rysunku 9.
Rysunek 10.
Rysunek 11.
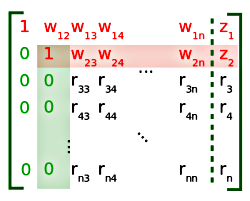
Postępujemy tak dalej z wierszem czwartym, piątym itd., otrzymując zera w całej kolumnie drugiej pod przekątną. Wynik widać na Rysunku 10.
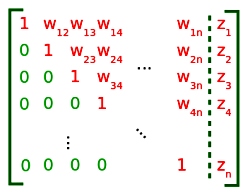
Kończymy w ten sposób drugi "krok" metody eliminacji Gaussa a w kolejnych "krokach", postępując tak samo, "produkujemy" jedynki na przekątnej części kwadratowej i zera poniżej. W końcu otrzymujemy docelową postać macierzy układu, przedstawioną na Rysunku 11. Opisany przez tę macierz układ daje się rozwiązać wprost "od dołu". Z ostatniego równania mamy xn = zn, potem wyliczamy xn-1 z wiersza poprzedniego itd.
Wybór elementu głównego
Rysunek 12.
Jak wspomnieliśmy wcześniej, w trakcie realizacji metody eliminacji Gaussa wymaga się, by napotykane na przekątnej współczynniki były wszystkie różne od zera, bo musimy przez nie dzielić kolejne wiersze.
Może się jednak oczywiście zdarzyć, że napotkany w kolejnym "kroku" metody współczynnik "przekątniowy" jest równy zeru! Nie oznacza to wcale, że układu nie umiemy rozwiązać!
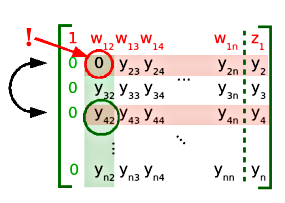
Przykład takiej sytuacji dla drugiego "kroku" metody ilustruje Rysunek 12. W tym momencie pojawia się konieczność modyfikacji metody eliminacji Gaussa o wybór elementu głównego.
Formalnie wystarczy, by wśród elementów drugiej kolumny poniżej przekątnej znaleźć przynajmniej jeden element niezerowy i zamienić miejscami odpowiednie wiersze. My dodatkowo poprawimy dokładność otrzymanego rozwiązania wyszukując każdorazowo wśród elementów poniżej przekątnej współczynnik największy co do modułu i zamieniając odpowiednie wiersze, oczywiście wraz z kolumną wyrazów wolnych (optymalnie napisany program nie zamienia zer, bo po co). Na Rysunku 12 pokazana jest sytuacja, gdy największy co do modułu współczynnik znaleziono w wierszu czwartym.
Postępować tak będziemy zawsze, nie tylko gdy napotkamy element zerowy na przekątnej. W ten sposób automatycznie znika zagrożenie dzielenia przez zero a dodatkowo otrzymane rozwiązanie jest dokładniejsze, gdyż unikamy szkodliwego ze względów numerycznych dzielenia przez małe liczby.
Taka metoda postępowania nazywa się częściowym wyborem elementu głównego. Pełny wybór realizowalibyśmy wyszukując współczynnika największego co do modułu nie tylko w kolumnie pod napotkanym zerem ale w całej podmacierzy "w dół i w prawo". Może to jeszcze poprawić dokładność ale jest znacznie bardziej czasochłonne, nie będziemy więc tej metody tu stosować.
A co zrobić, gdy wszystkie współczynniki na i poniżej przekątnej są zerami?!
Oznacza to po prostu, że dany układ nie posiada jednoznacznego rozwiązania lub jest sprzeczny. Wypisujemy odpowiedni komunikat i kończymy pracę programu. Pełny wybór elementu głównego nic tu nie pomoże.
Przykładowe zestawy danych testowych
