Autorem poniższego opracowania jest dr Piotr A. Dybczyński z Instytutu Obserwatorium Astronomiczne UAM w Poznaniu.
Pozycyjny system zapisu liczb
Powszechnie stosowany system dziesiętny zapisu liczb jest tzw. systemem pozycyjnym. Oznacza to, że wartość (waga) każdej z użytych cyfr, zależy od jej pozycji w liczbie.
Idąc od prawej strony mamy w każdej liczbie wielocyfrowej jednostki, dziesiątki, setki, tysiące itd. Dziesiętny system pozycyjny przypisuje każdej z cyfr w liczbie wagę równą odpowiedniej potędze podstawy systemu, czyli dziesiątki.
I tak, cyfra stojąca na skrajnej, prawej pozycji ma wagę (jest przy określaniu wartości liczby mnożona przez) 100 , czyli 1, jest to więc liczba jednostek.
Stojąca obok niej z lewej cyfra, ma wagę 101 , czyli 10, jest to więc liczba dziesiątek.
Ogólnie możemy powiedzieć, że jeżeli jakaś liczba jest w systemie dziesiętnym zapisana ciągiem cyfr, które oznaczymy jako
anan-1an-2 ... a2a1a0
to jej wartość wyliczamy ze wzoru:
an ×10n + an-1×10n-1 + an-2 ×10n-2 + ... + a2×102 + a1×102 + a0×100
Dla prostoty opisu zajmujemy się tylko liczbami całkowitymi, choć liczby ułamkowe w zapisie dziesiętnym są konstruowane analogicznie, tylko z ujemnymi potęgami dziesiątki w wagach cyfr po przecinku.
Liczby ujemne w tym zapisie oznaczamy specjalnym symbolem '-' (minus), stawianym przed całą liczbą.
System binarny jest skonstruowany dokładnie na tej samej zasadzie!
Różnica jest tylko jedna: podstawą systemu jest liczba 2, a w zapisie liczb występują tylko dwie cyfry, 0 i 1. Jest to również system pozycyjny, a więc o wadze każdej cyfry decyduje jej pozycja w liczbie binarnej (dwójkowej), liczona też od prawej strony.
Zamiast jednostek, dziesiątek, setek i tysięcy mamy tu: jednostki, dwójki, czwórki, ósemki itd. Np. liczba dwójkowa:
10010101001
ma wartość:
1×210 + 0×29 + 0×28 + 1×27 + 0×26 + 1×25 + 0×24 + 1×23 + 0×22 + 0×21 + 1×20
czyli w tym przypadku 1024+128+32+8+1 = 1193 w zapisie dziesiętnym. Liczba -1193 będzie miała postać -10010101001 .

Przykład pisemnego
dodawania i mnożenia
liczb w zapisie dwójkowym.
Działania na liczbach dwójkowych
Pisemne działania na liczbach w zapisie binarnym przeprowadzamy według tych samych zasad co na liczbach w zapisie dziesiętnym, pamiętając jedynie, że podstawą jest teraz dwa a nie dziesięć. Przykłady zapisów takich działań pokazane są na rysunku obok.
System binarny w komputerach
Liczby całkowite
zapisywane są w pamięci komputerów w systemie dwójkowym opisanym wyżej, są jednak pewne specyficzne różnice. System binarny wybrano, bo stosunkowo najprościej było użyć dwustanowych elementów elektronicznych do zapisania dwóch różnych cyfr. Jedną cyfrę dwójkową w pamięci komputera nazywamy bitem. Już bardzo dawno przyjęto, że najmniejszą, bezpośrednio adresowalną porcją pamięci, będzie oktet (czyli osiem) bitów, nazwany bajtem.
Tak więc pierwsza zauważalna różnica to fakt, że liczby binarne w pamięci komputera mają liczbę cyfr będącą całkowitą wielokrotnością ośmiu. Realizowane jest to poprzez dopisywanie nieznaczących zer po lewej stronie, tak by "dopełnić" skrajny, lewy bajt. Mówimy wręcz w żargonie komputerowym o liczbach jedno-, dwu- czy np. cztero-bajtowych. Takie sformułowanie od razu określa zakres możliwych do zapisania liczb poprzez ustalenie maksymalnej ilości cyfr dwójkowych.
I tak:
- w jednym bajcie możemy zapisać liczby z zakresu od 0 do 255
- w dwóch bajtach od 0 do 65535
- w czterech od 0 do 4294967295
- w ośmiu: 0 do 18446744073709551615
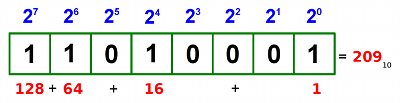
Bajt interpretowany jako liczba bez znaku.
No dobrze, a co ze znakiem? I tu pojawia się druga, znacznie ważniejsza różnica. Dla oszczędności miejsca w pamięci umówiono się, że zamiast stosować dodatkowy sposób sygnalizowania, że liczba jest ujemna, znak będzie kodowany na jednym z bitów. Aby jednak nie tracić tego bitu bezpowrotnie tylko na kodowanie znaku, przyjęto, że to procesor musi wiedzieć "z innych źródeł", czy w danym kawałku pamięci zapisaliśmy liczbę bez znaku (czyli na pewno dodatnią) lub ze znakiem (czyli dodatnią lub ujemną). Z samego zapisu binarnego nie sposób zgadnąć, o który wariant kodowania chodzi. Te "inne źródła" to najczęściej interpretacja domyślna w danej implementacji lub (np. w języku C) jawne deklarowanie wszystkich zmiennych jako "ze znakiem" lub "bez znaku".
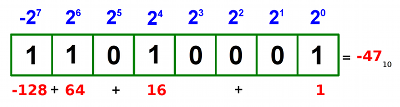
Bajt o tej samej zawartości, teraz
interpretowany jako liczba ze znakiem.
Najpowszechniejsza dziś umowa, tzw. kodowanie z uzupełnieniem do 2 ("Two's complement") mówi tak:
- jeśli ma być zapisana liczba bez znaku (unsigned) to stosujemy normalny zapis dwójkowy w ramach limitu narzuconego przez ilość bajtów, czyli w zakresach podanych wyżej.
- jeśli natomiast ma być zakodowana liczba ze znakiem to umawiamy się że waga najstarszego bitu zostaje pomnożona przez (-1). Dla liczb jedno-bajtowych oznacza to wagę -128 (-1×27), dla dwu-bajtowych -32768 (-1×215) itd.
Powoduje to w praktyce, dla liczb ze znakiem, przesunięcie podanych wyżej zakresów tak, by zero wypadło po środku:- w jednym bajcie możemy zapisać liczby ze znakiem z zakresu od -128 do +127
- w dwóch bajtach od -32768 do +32767
- w czterech od - 2147483648 do +2147483647
- w ośmiu: od -9223372036854775808 do +9223372036854775807

Dwa bajty interpretowane jako liczba bez znaku.

Dwa bajty o tej samej zawartości, teraz interpretowane jako liczba ze znakiem.
Jeszcze raz, dużymi literami: to procesor ma wiedzieć, jak zinterpretować ciąg bitów. Jeśli zastanie w jednym bajcie 11111111, to gdy ma to być liczba bez znaku, zapis ten zostanie zinterpretowany jako (dziesiętnie) 255, jeśli natomiast ma to być liczba ze znakiem, to wynosi ona -1 !! Jak widać różnica jest zasadnicza!
Taki sposób kodowania liczb ze znakiem ma jeszcze inne ciekawe i korzystne własności.
Liczby dwójkowe są bardzo często skrótowo zapisywane w systemie szesnastkowym.
Liczby zmiennoprzecinkowe
są również kodowane w pamięci komputerów za pomocą bitów. Powszechnie stosowany jest sposób zapisu opisany w standardzie IEEE-754.
Ponieważ nie będą nam potrzebne detale tego zapisu, ograniczymy się tu do podania jego podstawowych cech. Liczba zmiennoprzecinkowa pojedynczej precyzji (typ float w języku C) jest zapisywana w czterech bajtach, czyli 32 bitach.
Wygląda ona następująco (rys.):
ZWWWWWWWWMMMMMMMMMMMMMMMMMMMMMMM
Z jest bitem znaku całej liczby, zero oznacza liczbę dodatnią, jedynka - ujemną.
WWWWWWWW to osiem bitów wykładnika. Jest to liczba binarna bez znaku, od której odejmujemy 12710, uzyskując w ten sposób wykładniki z zakresu (dziesietnie) od -127 do +128.
MMMMMMMMMMMMMMMMMMMMMMM to 24 bity mantysy, interpretowanej jako część ułamkowa zmiennoprzecinkowej liczby binarnej: 1.MMMMMMMMMMMMMMMMMMMMMMM . Daje to w zapisie dziesiętnym ok. 7 cyfr znaczących.
Ostatecznie wartość liczby to: znak 1.mantysa razy 2wykładnik.
Tak określony sposób kodowania pozwala zapisać liczby zmiennoprzecinkowe pojedynczej precyzji z zakresu od 1.17549435 × 10-38 do 3.40282347 × 10+38 .
Liczba zmiennoprzecinkowa podwójnej precyzji (typ double w języku C) jest zapisywana w 8 bajtach, czyli 64 bitach. Budowa kodu jest podobna, jedynie wydłużają się wykładnik i mantysa. Wykładnik zajmuje 11 bitów, co pozwala zakodować wartości od -1023 do +1024. Część ułamkowa mantysy zajmuje 52 bity, dając w zapisie dziesiętnym 15-16 cyfr znaczących.
Tak określony sposób kodowania pozwala zapisać liczby zmiennoprzecinkowe podwójnej precyzji z zakresu od 2.2250738585072014 × 10-308 do 1.7976931348623157 × 10+308.
Jeśli kogoś bardziej interesuje ta tematyka, proponuję zajrzeć tu i do artykułu (po angielsku lub francusku) tam cytowanego.
Inny ciekawy materiał (po angielsku) jest tu.


