IV. WPŁYW PRZEJŚCIA GWIAZDY NA ODLEGŁOŚĆ PERIHELIUM KOMETY.
Jak już wspomnieliśmy wcześniej, głównym przedmiotem naszego zainteresowania jest wpływ oddziaływania grawitacyjnego przechodzącej gwiazdy na odległość perihelium komety.
Szczególnie interesują nas takie przypadki, w których następuje znaczne zmniejszenie tej odległości, stwarzające potencjalną możliwość zaobserwowania komety. Za kryterium obserwowalności komety przyjęliśmy w tej pracy warunek, aby jej odległość perihelium była mniejsza od 10 AU. Wartość ta jest podyktowana możliwościami współczesnych technik obserwacyjnych.
Należy jeszcze podkreślić, że w tej pracy nie rozważamy bezpośrednio kumulowanego rezultatu wielu przejść gwiazd, koncentrując się jedynie na efektach pojedynczego przejścia w zależności od parametrów ruchu gwiazdy ( masa, prędkość i odległość perihelium ) oraz od elementów orbity komety i jej pozycji na orbicie.
Warto dodać w tym miejscu, że wyniki prac dotyczących dynamicznej ewolucji dużej populacji komet pod wpływem wielu przejść gwiazdowych ( por.np. Remy i Mignard, 1985a; Duncan, Quinn i Tremaine, 1987 ) pokazują, że po pierwszym, często długo trwającym okresie ewoluowania populacji kometarnej, ustala się w przybliżeniu statyczny obraz, w którym następne przejścia gwiazd nie powodują już zauważalnych zmian rozkładów poszczególnych elementów orbit kometarnych w badanej populacji. W tym końcowym stadium wynik np. 100 przejść gwiazd traktowanych niezależnie będzie nieznacząco różnił się od skumulowanego efektu tych 100 przejść.
W rozważanym zagadnieniu zmiana orbity komety jest skutkiem
różnicowego wpływu grawitacyjnego przechodzącej gwiazdy na ruch
komety i Słońca. Obie składowe oddziaływania są tym silniejsze im
większa jest masa gwiazdy i im mniejsza jest jej prędkość. W obu
przypadkach decydującą rolę odgrywa jednak najmniejsza odległość
gwiazdy od zaburzanego ciała. Jeżeli gwiazda przechodzi daleko
od Słońca, to składowa słoneczna jest mała i znacząca zmiana orbity nastąpi tylko w przypadku komet znajdujących niezbyt daleko
od toru gwiazdy. Jeżeli natomiast gwiazda przechodzi blisko Słońca,
to człon słoneczny jest w większości przypadków dominujący i zmianie ulegną prawie wszystkie heliocentryczne orbity komet. Celowo
operujemy tu nieprecyzyjnymi określeniami: "blisko" czy "daleko",
gdyż konkretne granice silnie zależą od masy i prędkości gwiazdy,
co wyraźnie widać w przytoczonych dalej wynikach.
Jak to pokazaliśmy w poprzednim rozdziale całkowity efekt
oddziaływania gwiazdy można z dobrym przybliżeniem traktować jako
wynik impulsowej zmiany prędkości komety w chwili największego
zbliżenia z gwiazdą. Jeżeli minimalna odległość gwiazdy od komety
jest wystarczająco mała, to wartość tego impulsu jest porównywalna
a często nawet zdecydowanie większa od prędkości orbitalnej komety. Oznacza to, że przy takich ciasnych zbliżeniach orbita komety
może zmienić się drastycznie. Przypadki takie nie są rzadkością,
zważywszy na wielką liczebność komet wynikającą ze współczesnych
szacunków ( rzędu 1012 ) i fakt, że minimalna odległość gwiazdy
od Słońca może być mniejsza od promienia obłoku kometarnego.
Są one tym prawdopodobniejsze, im większy jest stosunek masy gwiazdy do jej prędkości.
Poniżej pokażemy na szeregu przykładach, jak zmienia się odległość perihelium komety pod wpływem przejścia gwiazdy. W pierwszej kolejności zajmiemy się dwoma konfiguracjami, w których wektor zmiany prędkości komety leży w płaszczyźnie jej ruchu niezaburzonego. Ma to miejsce gdy tor gwiazdy leży w płaszczyźnie ruchu komety lub gdy ta płaszczyzna jest prostopadła do toru gwiazdy.
W takich przypadkach jedynym skutkiem oddziaływania gwiazdy będzie zmiana kształtu orbity komety, bez zmiany orientacji płaszczyzny jej ruchu. Należy spodziewać się, że w takich sytuacjach najczęściej występować będzie radykalne zmniejszenie odległości perihelium komety.
W dalszej części rozdziału pokażemy przebieg zmian odległości perihelium komety w innych konfiguracjach a kilka kolejnych przypadkowych orientacji zamieściliśmy w rozdziale piątym.
PRZEJŚCIE GWIAZDY W PŁASZCZYŹNIE ORBITY KOMETY.
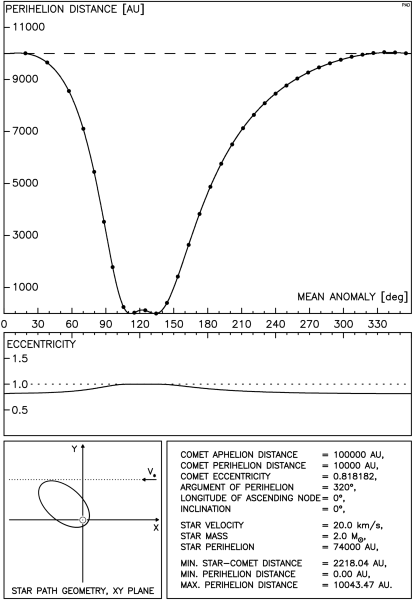
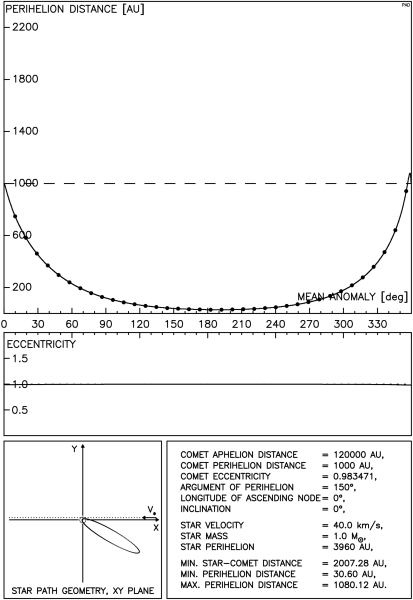
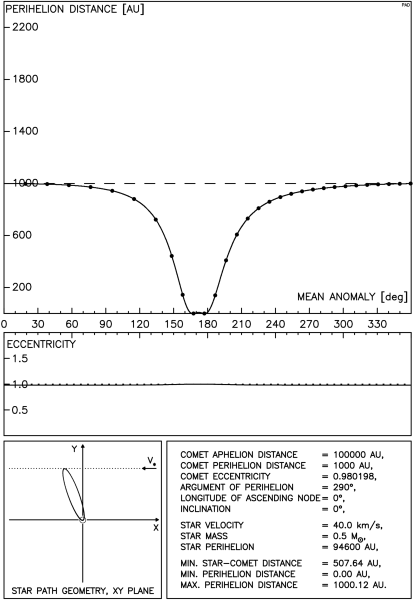
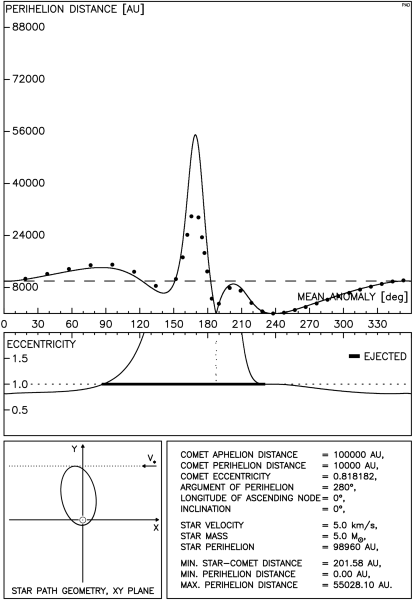
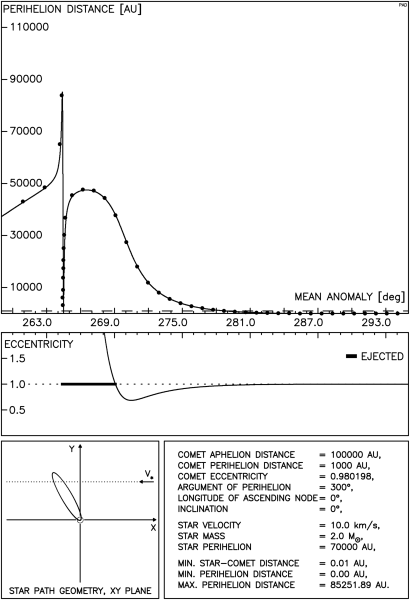
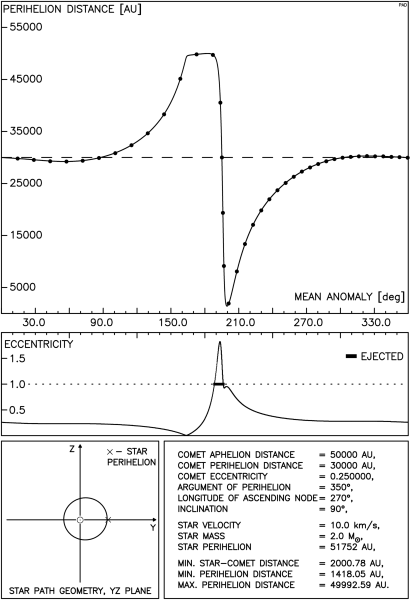
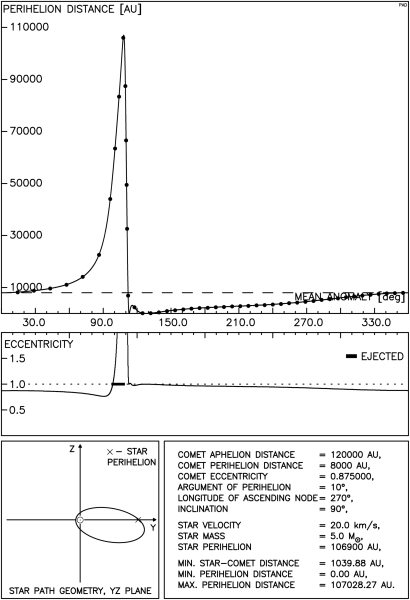
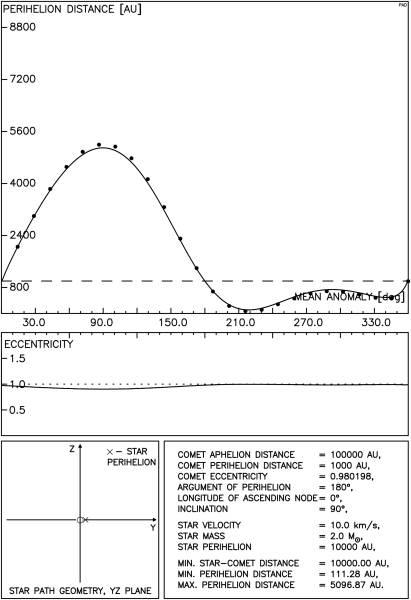
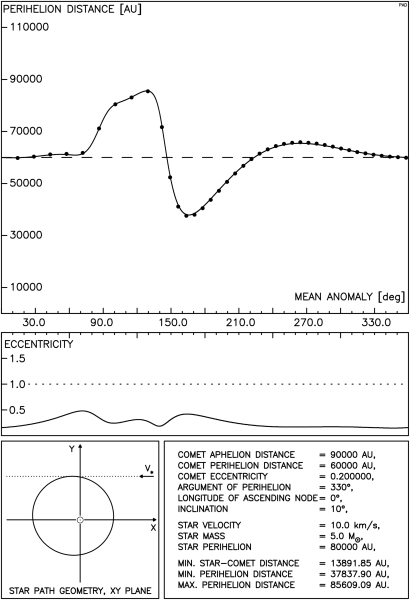
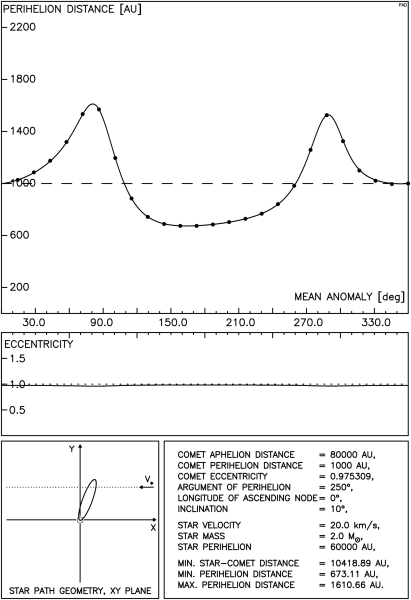
Istnieją tu dwie, jakościowo różne sytuacje: gdy gwiazda przechodzi poza orbitą komety oraz gdy tor gwiazdy przecina tę orbitę. Przykładowy przebieg zmian odległości perihelium komety w tej pierwszej sytuacji przedstawia rysunek 4.1. Odległość między orbitami gwiazdy i komety wynosi tu ok. 2200 AU i jest wystarczająco mała, aby możliwe było zredukowanie odległości perihelium komety poniżej granicy obserwowalności. Postać rysunku została już szczegółowo opisana wcześniej, przypomnijmy jedynie, że ciągła linia na górnym wykresie pokazuje wyniki otrzymane przy pomocy pełnej metody impulsowej natomiast punkty oznaczają wartości uzyskane z całkowania numerycznego.
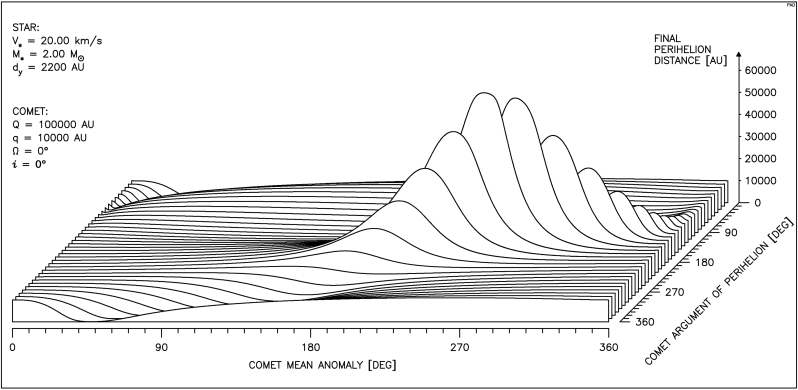
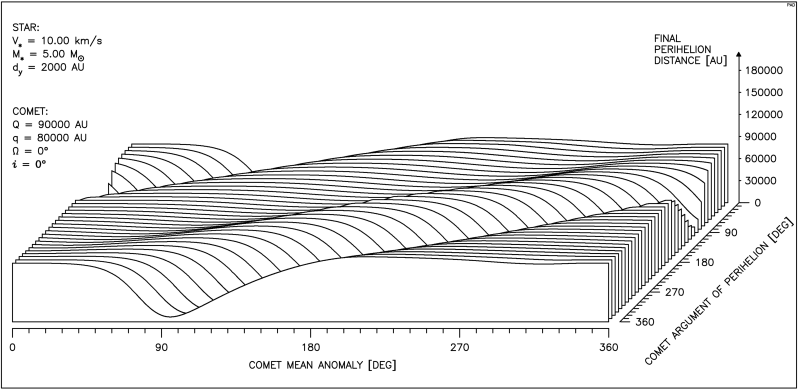
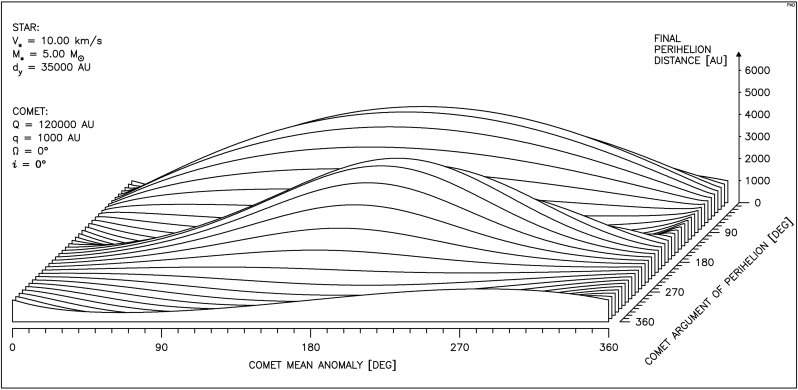
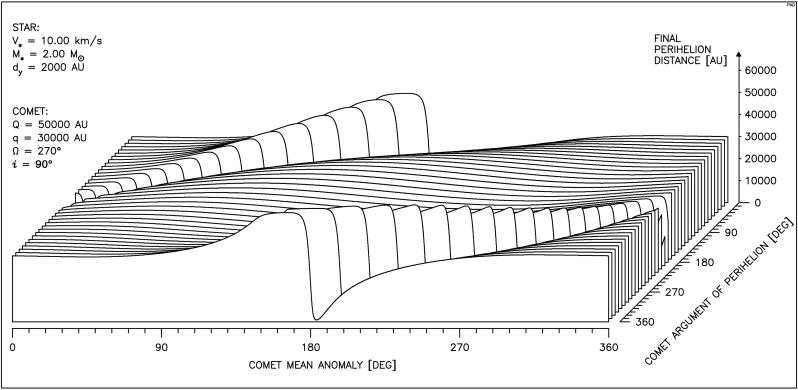
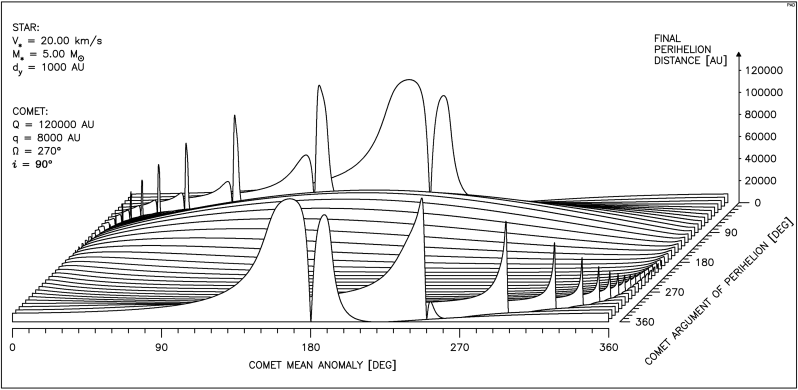
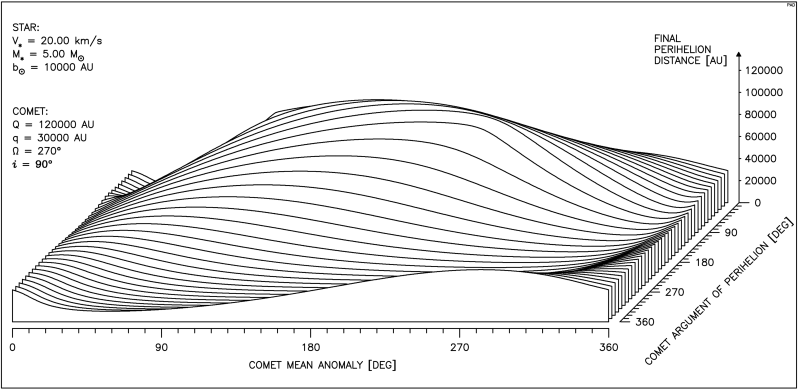
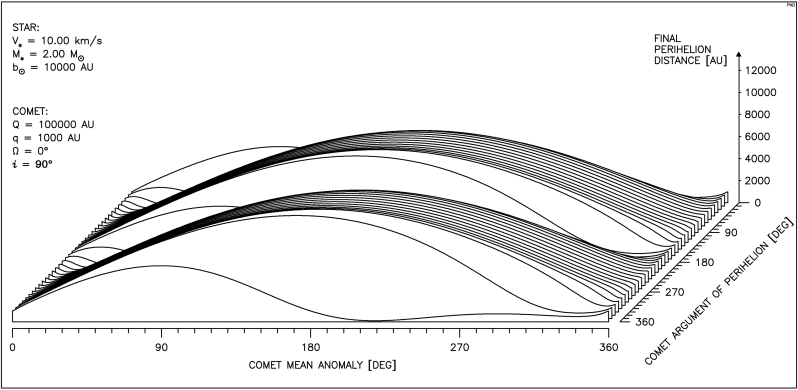
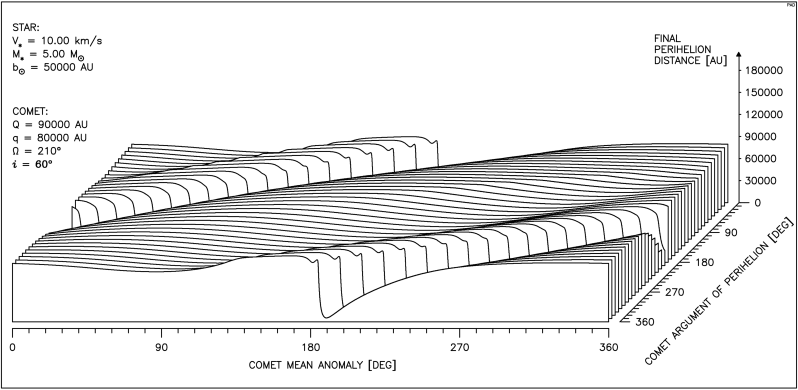
Aby uzyskać pełen obraz zależności przebiegu zmian odległości perihelium komety od parametrów ruchu gwiazdy oraz anomalii średniej i argumentu perihelium komety, należałoby przedstawić kilkadziesiąt takich wykresów. Dlatego posłużymy się tu inną postacią wykresu, uwzględniającą oprócz zależności od anomalii średniej komety, również zależność od argumentu perihelium. Taki pseudo przestrzenny rysunek pokazuje, jak zmienia się wpływ przejścia gwiazdy na odległość perihelium komety gdy zmieniamy jednocześnie oba wymienione parametry kątowe. Ze względu na okresowy ich charakter prawa krawędź rysunku jest identyczna z lewą a pierwszy przebieg jest powtórzony w tyle. W lewym, górnym rogu każdego wykresu wypisane są najważniejsze parametry, stałe dla wszystkich 36 krzywych tworzących rysunek. Objaśnienia wymaga parametr dy pojawiający się tu po raz pierwszy. Otóż aby lepiej pokazać zależność badanego efektu od obu wymienionych parametrów kątowych dla każdego przebiegu ( czyli dla każdej wartości argumentu perihelium komety) dobierana jest taka odległość toru gwiazdy od Słońca, aby najmniejsza odległość gwiazdy od orbity komety była stała dla wszystkich wartości argumentu perihelium. Właśnie ta ostatnia odległość została oznaczona jako dy .
Wśród krzywych tworzących rysunek 4.2 jest krzywa przedstawiona na rysunku 4.1.
Dla zwiększenia przejrzystości tekstu będziemy w opisach rysunków posługiwać się oznaczeniem q dla odległości perihelium komety, będziemy też anomalię średnią komety oznaczać przez M , a argument perihelium komety przez ω.
Na rysunku 4.2 widzimy przebieg zmian q dla gwiazdy o typowej prędkości i masie równej podwójnej masie Słońca.
Dla 360° > ω > 270° widać obszary znacznego zmniejszenia q, natomiast dla 270° > ω > 90° obszary znacznego wzrostu q.
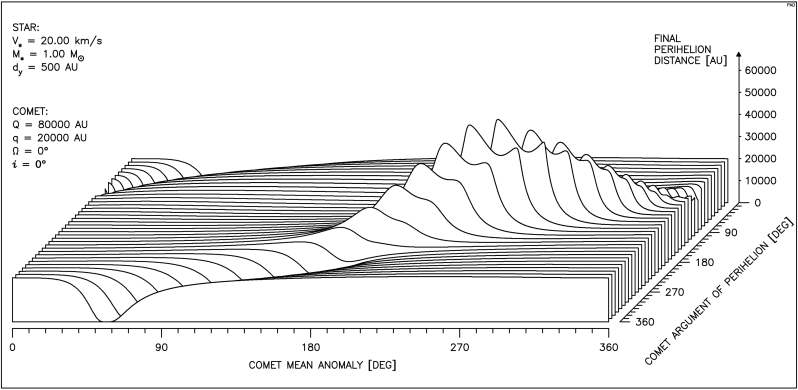
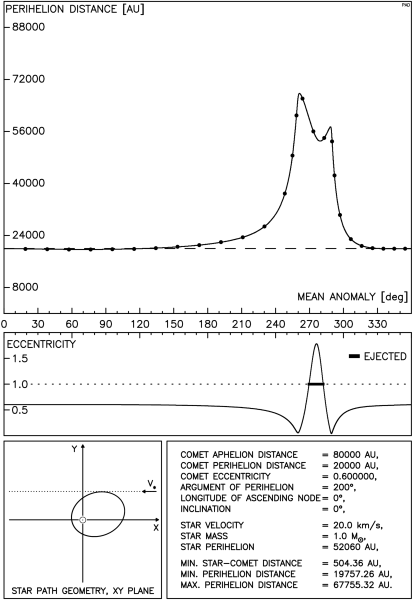
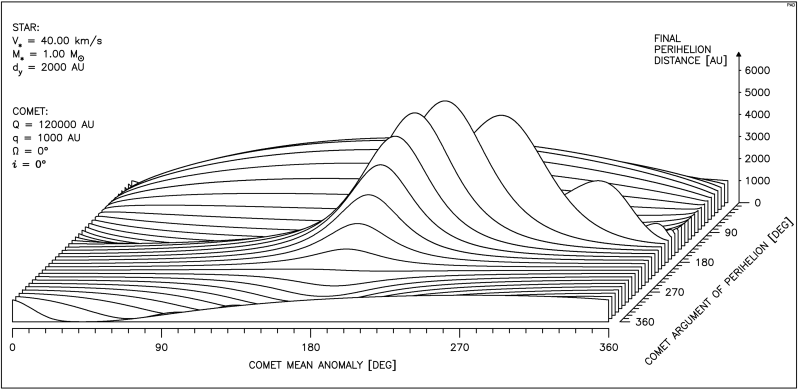
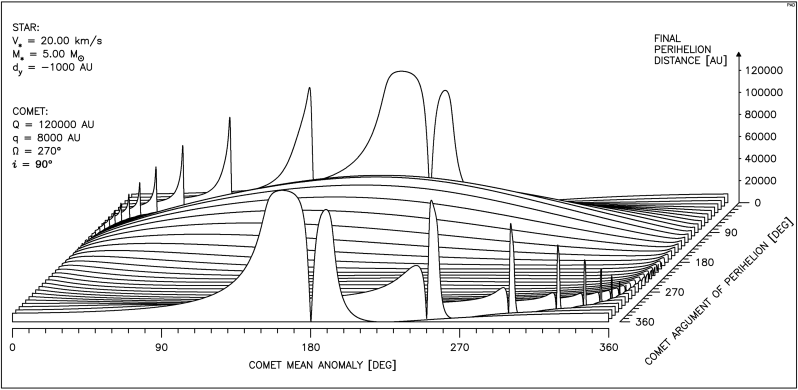
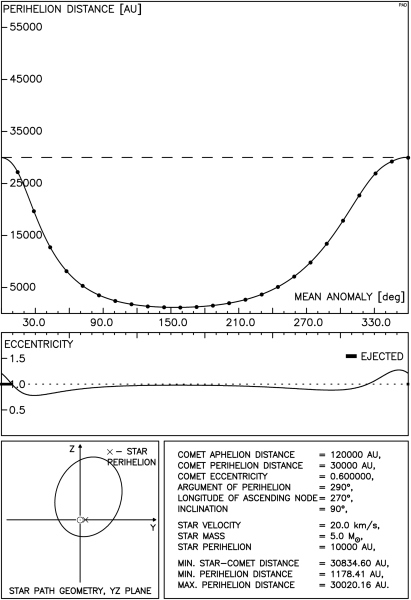
Rysunek 4.3 dotyczy komety o mniejszej i mniej wydłużonej orbicie, prędkość gwiazdy jest ta sama, natomiast jej masa jest równa masie Słońca. Ponieważ jednak minimalną odległość gwiazdy od komety zmniejszyliśmy do 500 AU, widać wyraźnie silniejsze oddziaływanie,a na niektórych krzywych pojawiają się ostrza. Jak to wyjaśnia rysunek 4.3a są to miejsca, w których mimośród orbity komety staje się bliski zeru i następuje gwałtowna zmiana położenia punktu perihelium. Odcinek pomiędzy ostrzami to obszar gwałtownego wzrostu mimośrodu aż do hiperbolicznego wyrzutu komety z obłoku.
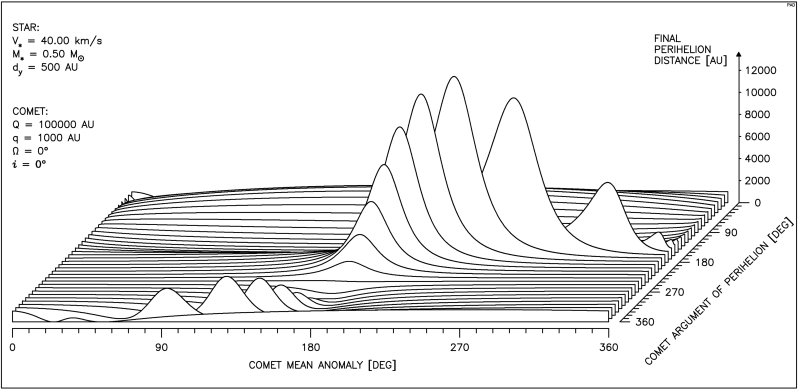
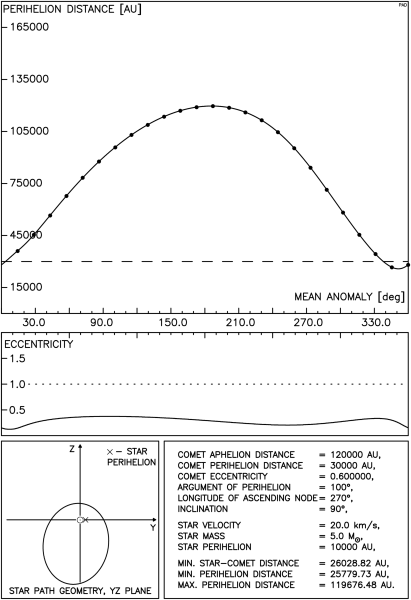
Rysunek 4.4 przedstawia zmiany q dla orbity prawie kołowej, dla masywnej i powolnej gwiazdy. Na orbicie o małym mimośrodzie nie jest oczywiście możliwe znaczne zwiększenie q , natomiast obszary jego zmniejszenia są przy tak silnym oddziaływaniu bardzo rozległe. Przejście mniej masywnej i szybszej gwiazdy powoduje dla takiej orbity znacznie słabszy efekt.
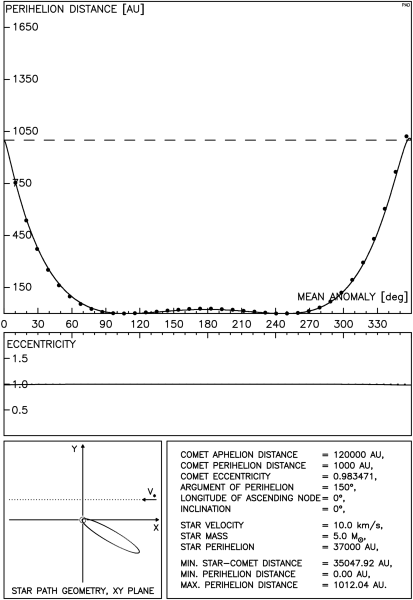
Jednakże nawet gwiazda o typowej masie, poruszająca się z prędkością 40 km/s względem Słońca może radykalnie zmienić q na or bicie o dużym mimośrodzie. Widać to na rysunku 4.5. Możliwe jest w tym przypadku powstanie orbity obserwowalnej.
W związku z tym rysunkiem ( i kilkoma w dalszej części rozdziału ) należy się pewne wyjaśnienie. Wprawdzie na początku pracy zastrzegaliśmy, że nie rozpatrujemy przejść gwiazd w odległościach mniejszych niż 10000 AU od Słońca jednakże, dla kompletności wykresów naruszyliśmy tę umowę. Stosowana w obliczeniach pełna metoda impulsowa uwzględnia efekty związane z bliskim przejściem tak obok komety jak i Słońca, dając również w tym ostatnim przypadku poprawne wyniki.
Potwierdza to w pełni wykres porównawczy zamieszczony na Rys 4.5a. Odległość gwiazdy od Słońca wynosi tu ok 4000 AU a na Rys 4.5 , dla ω = 90° spada nawet do 3000 AU.
Mimo iż w konfiguracji na rysunku 4.5a kometa w aphelium jest odległa od gwiazdy o ok. 50000 AU, to efekt zmniejszenia q jest wyraźnie widoczny. Mamy tu przypadek zdecydowanej dominacji członu słonecznego na prawie całej orbicie komety.
Rysunek 4.6 przedstawia efekt bliskiego przejścia szybkiej gwiazdy o małej masie. Obszar dominacji członu słonecznego jest tu słabo zaznaczony, występują jednak znaczne zmiany q w sprzyjających warunkach geometrycznych. Możliwe jest powstanie orbity obserwowalnej co potwierdza Rys. 4.6a. Jest to ważny wynik, ponieważ w otoczeniu Słońca jest wyraźnie więcej gwiazd o małych masach i prędkościach ok. 20 - 30 km/s.
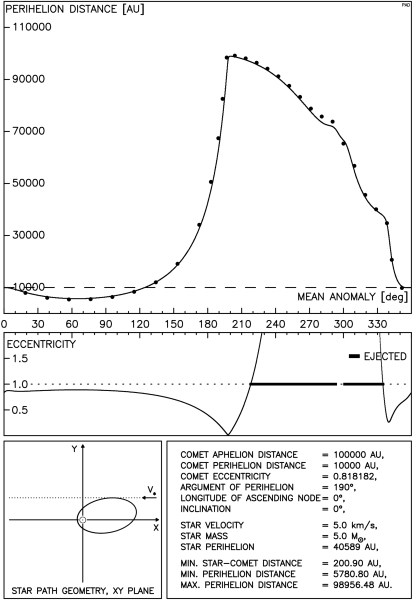
Na rysunku 4.7 pokazano wynik oddziaływania na kometę powolnej, masywnej gwiazdy, przechodzącej w znacznej odległości.
Dla 360° > ω > 180° mamy obszar dominacji członu kometarnego, dla pozostałych wartości ω dominującą rolę odgrywa człon słoneczny. Wynik ten pokazuje, że przejście takiej masywnej gwiazdy przez obłok kometarny powoduje znaczne zmiany orbit komet z odległości dziesiątków tysięcy AU. Mogą w ten sposób powstać również orbity o q < 10 AU, co potwierdza rysunek 4.7a. Warto podkreślić, że taka redukcja q występuje nawet wtedy, gdy odległość gwiazdy od komety wynosi ok. 100000 AU. Efekty pokazane na rysunkach 4.6 i 4.7 byłyby mniejsze dla orbit komet o mniejszych mimośrodach.
Można również na rys . 4.7a dostrzec pierwsze niezgodności rezultatów całkowania numerycznego i metody impulsowej. Masa gwiazdy jest tu jednak największa z rozważanych, a prędkość bliska dolnej granicy przedziału przyjętego do rozważań.
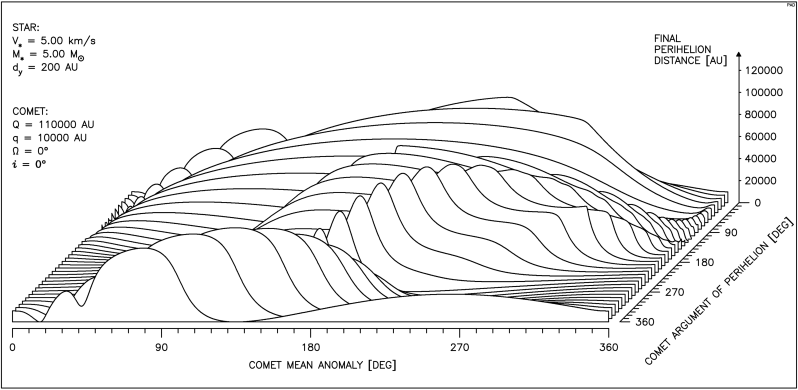
Rys.4.8. Przypadek bardzo silnego oddziaływania gwiazdy na kometę.
Masywna gwiazda przechodzi z małą prędkością bardzo blisko komety. Por. Rys. 4.8a i 4.8b.
Skrajny przypadek prezentuje rysunek 4.8. Masywna, powolna gwiazda przechodzi bardzo blisko komety. Widać, że przebieg zmian q znacznie się skomplikował i silnie zależy od konfiguracji geometrycznej. Oczywiście jeszcze silniejsze zmiany wystąpiłyby dla orbity o większym mimośrodzie ale wtedy wykres stałby się już jednak nieczytelny. Metoda impulsowa daje ciągle jeszcze dość dobre wyniki ( por. rysunki 4.8a i 4.8b ), choć w pewnych przypadkach pojawiają się już duże różnice. Przebiegi otrzymywane dwoma metodami są jednak nadal podobne, a co ważniejsze różnice są wyraźnie mniejsze, gdy następuje zmniejszenie q .
Efekt ten jest potwierdzony na wielu przykładach i bierze się stąd, że zmniejszenie q prawie nigdy nie wynika z silnego oddziaływania na małej odległości, ale ze zmniejszenia prędkości komety do bardzo małej wartości, co wymaga określonej konfiguracji geometrycznej. Mniej istotna jest długość wektora impulsu prędkości, ważny jest natomiast jego kierunek, zgodny z kierunkiem prędkości komety na orbicie niezaburzonej.
Wniosek ten jest dla nas ważny, ponieważ w rachunkach następnego rozdziału opieramy się prawie wyłącznie na metodzie impulsowej. Dodatkowe uwagi o zgodności całkowania numerycznego i metody impulsowej w przypadkach zmniejszenia q poniżej 10 AU można znaleźć w rozdziale piątym.
W przypadku płaskim pozostały nam do omówienia takie konfiguracje geometryczne, w których tor gwiazdy przecina orbitę komety.
Z punktu widzenia badania stosowalności metody impulsowej są to przypadki interesujące, ponieważ odległość gwiazdy od komety spada tu do zera. Możemy więc na jednym wykresie obserwować zależność błędu metody impulsowej od tej odległości. Z punktu widzenia praktycznych zagadnień są to jednak przypadki tak mało prawdopodobne, że ograniczymy się tylko do kilku przykładów.
Dodajmy jeszcze, że wyniki przedstawione powyżej zachowują swoją ważność również dla komet o orbitach z niewielkim nachyleniem w stosunku do płaszczyzny ruchu gwiazdy. Efekty przejścia są tylko wtedy nieco mniejsze, natomiast pokazane niżej przypadki przecinania orbity komety przez gwiazdę wymagają ścisłego pokrywania się płaszczyzn ruchu lub, przy niezerowym nachyleniu, niemal trafienia gwiazdą w kometę.
Ze względu na charakter zmienności q przedstawienie na jednym wykresie zależności od M i ω uczyniłoby rysunek całkowicie nieczytelnym. Dlatego stosujemy tu jedynie wykresy w podstawowej postaci.
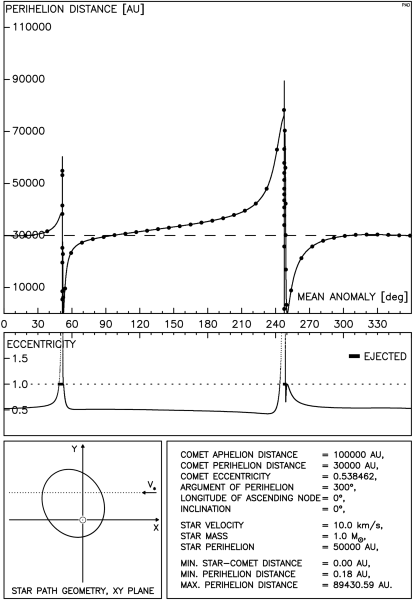
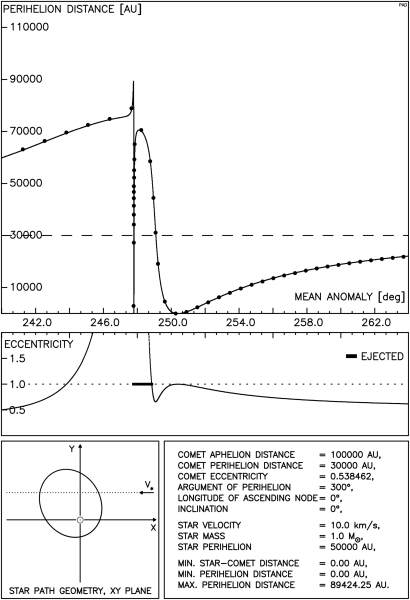
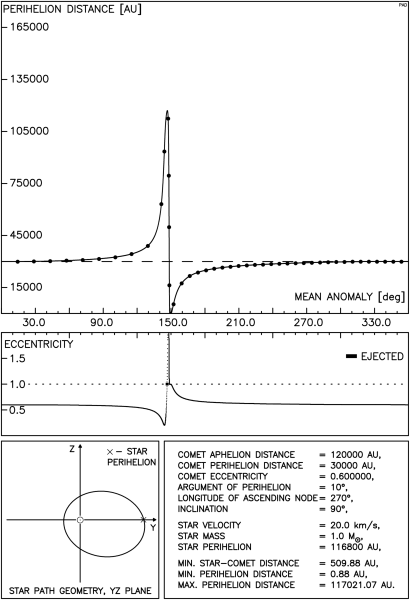
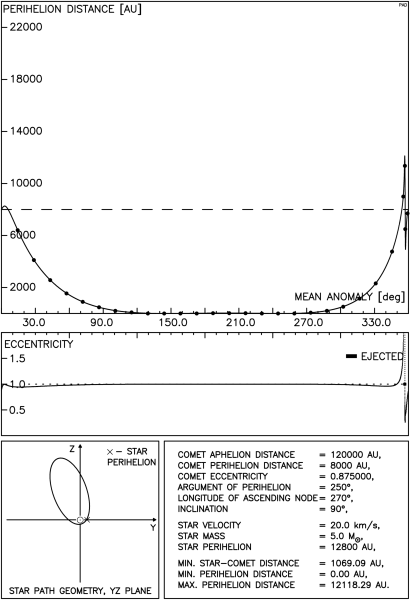
Rysunek 4.9 przedstawia typowy przebieg zależności q od M. Ponieważ interesujące partie takiego wykresu są bardzo zagęszczone, na następnych trzech rysunkach przedstawiamy jedynie otoczenie punktów przecięcia orbity komety przez tor gwiazdy. Rysunek 4.9a przedstawia w większej skali otoczenie jednego z takich punktów, pokazanych na rys.4.9.
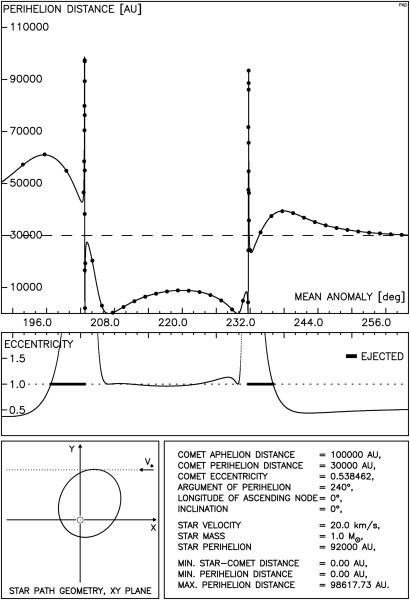
Dwa inne przypadki prezentujemy na rysunkach 4.10 i 4.11 . Nie widać na tych rysunkach istotnych różnic pomiędzy całkowaniem numerycznym a pełnym przybliżeniem impulsowym, pomimo iż dotyczą przypadków przecinania orbity komety przez tor gwiazdy.Oczywiście na pionowych odcinkach różnice występują zawsze gdyż metoda impulsowa nie daje dobrych wyników dla odległości bliskich zeru. Na wykresach objawia się to nierównomiernym rozkładem punktów oznaczających wyniki całkowania na krzywej otrzymanej metodą impulsową. Poza odcinkami pionowymi pewne różnice widać dopiero w przypadku masywnej gwiazdy przechodzącej z niedużą prędkością blisko komety.
PRZYPADEK PŁASZCZYZNY ORBITY KOMETY PROSTOPADŁEJ DO TORU GWIAZDY
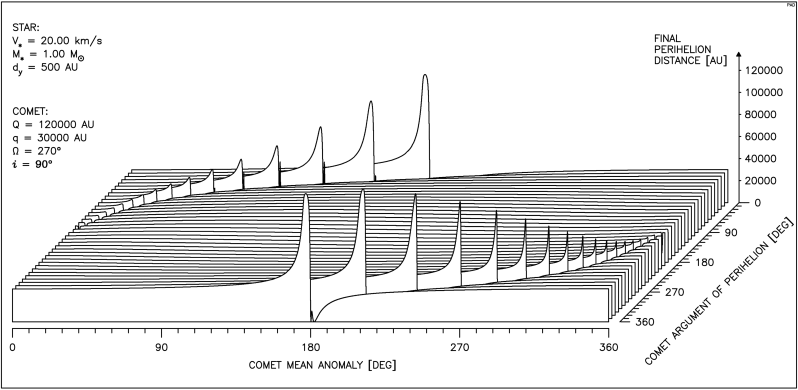
Rys.4.12. Przejście typowej gwiazdy blisko orbity komety.
Gwiazda przechodzi na zewnątrz orbity ( dy > 0 ).
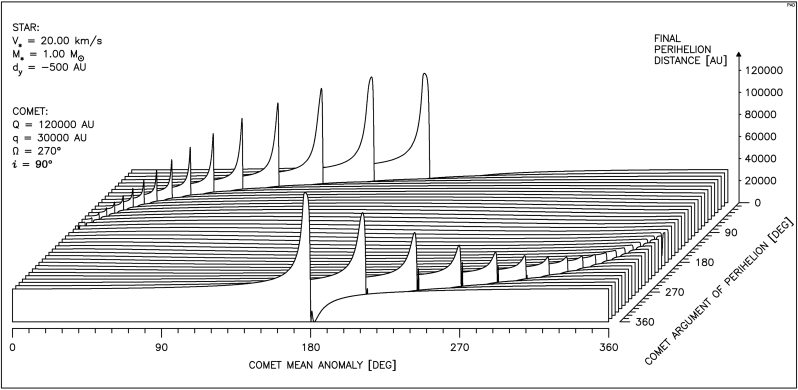
Rys.4.12a. Przejście typowej gwiazdy blisko orbity komety.
Gwiazda przechodzi po wewnętrznej stronie orbity.
Konfiguracja geometryczna w tym przypadku oznacza, że gwiazda przecina prostopadłą do swego toru płaszczyznę orbity komety. Oddziaływanie gwiazdy skupia się wyraźnie na odcinku orbity najbliższym toru gwiazdy. Tak jak w przypadku płaskim nie zmienia ono orientacji płaszczyzny orbity komety. Możliwe są przejścia gwiazdy zarówno na zewnątrz orbity komety jak i wewnątrz niej.
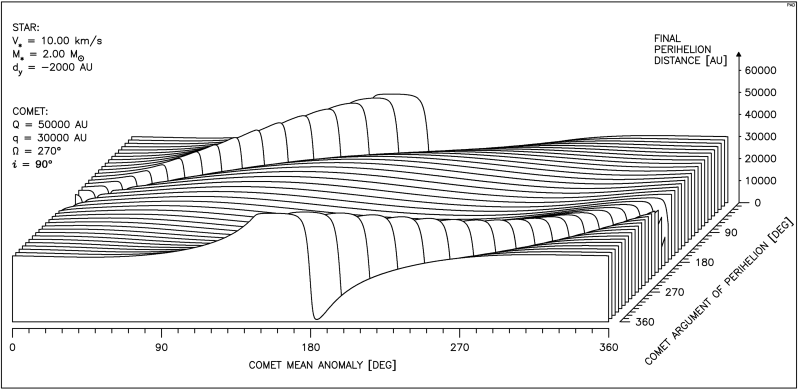
Jeżeli gwiazda przechodzi niezbyt daleko od orbity, to efekty obu tych typów przejść są bardzo podobne. Potwierdzają to wykresy zamieszczone na następnych stronach, ułożone w pary różniące się tylko znakiem wartości dy. Minus oznacza tu przejście po wewnętrznej stronie orbity.
Na rysunkach 4.12 i 4.12a widać rezultaty przejścia gwiazdy o typowych dla galaktycznego otoczenia Słońca parametrach, w nie wielkiej odległości od wydłużonej orbity komety. Łatwo dostrzec, że charakter oddziaływania nie jest zależny od wartości ω , zmienia się tylko jego siła. Zmiana q występuje jedynie dla tych wartości M , które opisują fragment orbity najbliższy toru gwiazdy. Rysunek 4.12a potwierdza, że nie ma zasadniczych różnic dla obu typów przejść. Dla każdej wartości ω pojawia się na obu rysunkach obszar zwiększania q oraz obszar wyraźnego zmniejszenia tej wartości. Rysunek 4.12c pokazuje jedną z krzywych tworzących rysunek 4.12a, na której widać przedział M odpowiadający obszarowi powstawania orbit obserwowalnych.
Długość węzła wstępującego orbity komety ustaliliśmy na tych i kilku następnych rysunkach na 270° dla zwiększenia przejrzystości wykresów. Wobec okresowości M i ω spowodowało to jedynie rozsunięcie na rysunkach obszarów silnego oddziaływania gwiazdy.
Należy też podkreślić, że pokazane w tym miejscu wyniki zachowują w pełni swoją ważność również dla orbit o nachyleniach równych 90° ± 20° i o liniach węzłów przecinających tor gwiazdy pod kątem 90° ± 30°.
Zmiany w stosunku do przypadku ściśle prostopadłego są niewielkie i na ogół polegają na pewnym osłabieniu oddziaływania.
Na rysunkach 4.13 , 4.13a i 4.13b przedstawiliśmy efekty przejścia masywnej gwiazdy o niewielkiej prędkości. Gwiazda przechodzi niezbyt blisko prawie kołowej orbity komety. Tak jak i poprzednio widać koncentrację większych zmian q na niewielkich przedziałach M , opisujących bliskie toru gwiazdy łuki orbity komety. Mimo iż najmniejsza odległość gwiazdy od komety jest czterokrotnie większa niż na Rys.4.12 to nadal nie widać istotnych różnic pomiędzy przejściem po wewnętrznej i po zewnętrznej stronie orbity. Prawie dla wszystkich wartości ω widać obszary radykalnego zmniejszenia q . Płaskie odcinki poszczególnych wykresów odpowiadają przedziałom M , w których q osiąga wartość maksymalną, równą odległości aphelium orbity wyjściowej, co widać wyraźnie na rysunku 4.13b.
Rysunki 4.14 i 4.14a-c przedstawiają wyniki silnego oddziaływania gwiazdy na orbitę komety o dużym mimośrodzie.
Podstawowe cechy omawianej zależności zmian q od M i ω pozostają niezmienione. Wyraźniej zaznacza się różnica pomiędzy przejściem wewnętrznym i zewnętrznym, widoczna jest jednak pewna symetria tych dwóch przypadków.
Nowym efektem jest wyraźnie zaznaczony obszar dominacji członu słonecznego dla 270° > ω > 90° . Występują dla tych wartości duże przedziały M, w których w wyniku oddziaływania gwiazdy na Słońce powstają orbity obserwowalne ( por. Rys.4.14b ).
Rysunek 4.14c pokazuje szczegółowo silne zmiany q dla gwiazdy przechodzącej w pobliżu aphelium orbity komety.
Kończąc omawianie przypadków, w których płaszczyzna orbity komety jest prostopadła do orbity gwiazdy w punkcie perihelium tej orbity, pragniemy zwrócić uwagę na lepszą zgodność metody impulsowej i całkowania numerycznego w przedstawionych przypadkach w stosunku do zagadnienia płaskiego.
Własność ta, potwierdzona innymi, niezamieszczonymi tu przykładami wynika z tego, że gwiazda przed i po momencie największego zbliżenia do komety i Słońca oddziaływuje prawie prostopadle do płaszczyzny orbity komety.
Powoduje to nieznaczną tylko zmianę najmniejszej odległości od komety w stosunku do jej ruchu niezaburzonego, co wyraźnie zbliża do siebie wyniki otrzymywane tymi dwoma metodami.
INNE KONFIGURACJE GEOMETRYCZNE.
Zanim przedstawimy na kilku przykładach wpływ przejścia gwiazdy na orbity o dowolnej orientacji, pozostańmy jeszcze przez chwilę przy nachyleniu bliskim 90° . We wszystkich omawianych dotąd przy padkach dobieraliśmy dla każdej wartości ω taką odległość asymptoty ruchu gwiazdy bo , aby najmniejsza odległość od komety była w przybliżeniu stała. Odejdziemy teraz od tej zasady, aby pokazać skutki przejścia gwiazdy blisko Słońca. Płaszczyzna orbity komety będzie jeszcze w tym przypadku prostopadła do toru gwiazdy.
Na rysunku 4.15 przedtawiamy zmianę q w zależności od M oraz ω dla stałej wartości bo = 10000 AU.
Jest to przejście masywnej gwiazdy o typowej prędkości. Widać, że wszędzie wyraźnie dominuje człon słoneczny. Dzieje się tak dlatego, że najmniejsza odległość gwiazdy od komety jest conajmniej dwukrotnie większa od odległości od Słońca. Dwie krzywe z tego rysunku są szczegółowo przedstawione na rysunkach 4.15a i 4.15b. Oczywiście bardzo podobny obraz zmian q będzie miał miejsce dla orbit komet o płaszczyznach prawie prostopadłych.
Na rysunku 4.16 orbita komety ma nadal nachylenie równe 90° lecz jej płaszczyzna jest teraz równoległa do wektora prędkości gwiazdy w punkcie przysłonecznym. Odległość gwiazdy od płaszczyzny orbity komety, a zarazem od Słońca, jest stała i wynosi 10000 AU.
Prawie na całym rysunku widać powiększenie q na skutek prostopadłego do orbity komety impulsu prędkości otrzymanego przez Słońce. Jedynie w punktach orbity najbliższych toru gwiazdy odległość gwiazda-kometa spada również do 10000 AU i oddziaływanie gwiazdy na Słońce i kometę jest równie silne. Przypadek, w którym gwiazda przechodzi dokładnie równolegle do linii absyd orbity komety, jest szczegółowo pokazany na rysunku 4.16a. Na tej połowie orbity, gdzie ruch komety jest zgodny z ruchem gwiazdy następuje zmniejszenie q , natomiast tam, gdzie ruch jest wsteczny, q się powiększa. Taki przebieg zmian q ma miejsce dla nachyleń orbity z przedziału ( 45° ,135° ). Gdy kometa znajduje się dokładnie w perihelium lub aphelium zmiana q nie występuje, o czym była mowa w rozdziale trzecim ( por Rys.3.8 ).
Na zakończenie tego przeglądu różnych konfiguracji geometrycznych przedstawimy jeszcze dwie z nachyleniem 10° i jedną o nachyleniu orbity komety równym 60° .
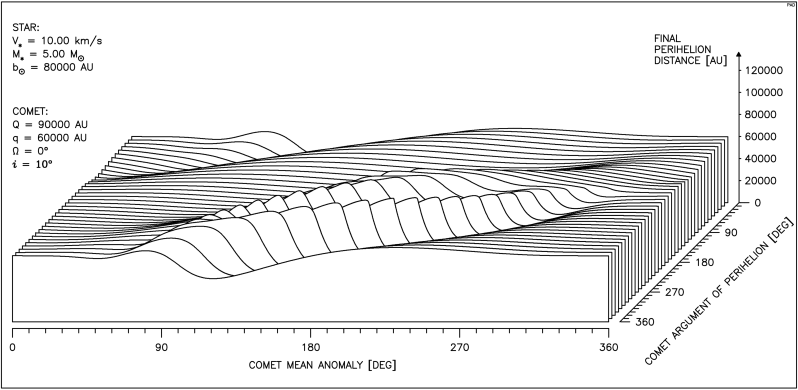
Na rysunku 4.17 widzimy skutki przejścia gwiazdy silnie oddziaływującej na orbitę o małym nachyleniu i mimośrodzie.
Wykres ten jest zgodnie z oczekiwaniem podobny do wykresu przedstawionego na rysunku 4.4. Parametry przechodzącej gwiazdy są w obu przypadkach takie same, jednakże pewne nachylenie orbity na rys. 4.17, jak i stała w tym przypadku minimalna odległość gwiazdy od Słońca, powodują pewne różnice przebiegów.
Jedną z krzywych tworzących rys. 4.17 przedstawiamy szczegółowo na Rys.4.17a.
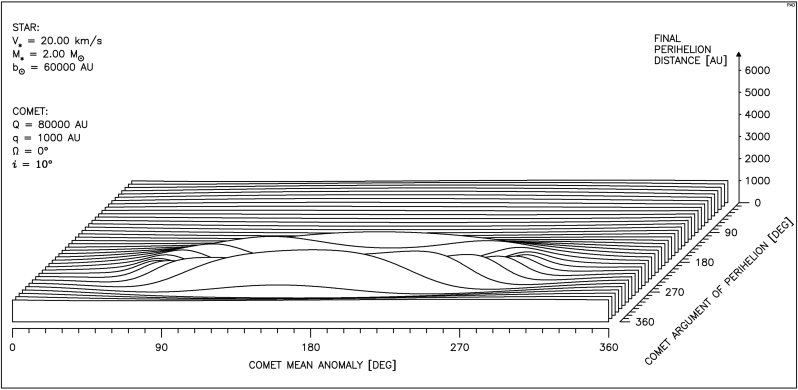
Przypadek orbity o tym samym nachyleniu ale większym mimośrodzie jest przedstawiony na rysunku 4.18. Skutki oddziaływania gwiazdy są widoczne tylko tam, gdzie zbliża się ona do okolic aphelium orbity komety. Przykład takiego przebiegu stanowi treść rysunku 4.18a. Orbita komety znajduje się tu nieco powyżej toru gwiazdy.
Rysunek 4.19, kończący ten rozdział, przedstawia prawie kołową orbitę ustawioną ukośnie do toru gwiazdy, która przechodzi wewnątrz tej orbity. Tak jak w wielu poprzednich przykładach znacząca zmiana q występuje na tych wycinkach orbity komety, które są zbliżone najbardziej do toru gwiazdy.
Przedstawione w tym rozdziale przykłady nie wyczerpują oczywiście wszystkich możliwości, jednak na tle wielu innych zbadanych przez nas przypadków, prezentują zbiór typowych zależności zmian q od parametrów ruchu gwiazdy, elementów orbity komety i konfiguracji geometrycznej przejścia.
Wykresy pokazujące zależność od obu parametrów ( M i ω ) dają pełny obraz dla ustalonej orientacji płaszczyzny orbity komety względem płaszczyzny ruchu gwiazdy. Pozostałe rysunki pozwalają lepiej przeanalizować poszczególne przypadki, są też kolejnym elementem porównania wyników pełnej metody impulsowej z rezultatami całkowania numerycznego. W następnym rozdziale pokażemy jeszcze kilka takich szczegółowych wykresów dla zupełnie przypadkowych konfiguracji, uzyskanych z symulacji numerycznej przelotu gwiazdy przez obłok kometarny.