III. STOSOWALNOŚĆ PRZYBLIŻENIA IMPULSOWEGO.
W tym rozdziale przedyskutujemy stosowalność metody impulsowej w różnych postaciach, opierając się głównie na porównaniu otrzymywanych wyników z rezultatami całkowania numerycznego. Porównanie takie można przeprowadzić wyznaczając dwoma metodami przyrost prędkości komety lub porównując elementy orbity otrzymane dla tych dwóch wartości prędkości i nie zmienionego położenia. Pierwszy sposób pozwala bezpośrednio oszacować błąd stosowanego przybliżenia, natomiast drugi pokazuje wpływ tego błędu na szukaną wartość, którą w tej pracy jest najczęściej odległość perihelium komety.
Z punktu widzenia celu niniejszej pracy wydaje się, że ta druga metoda porównywania jest pełniejsza, dlatego jest ona stosowana w większości prezentowanych niżej rozważań.
Dotychczas opublikowano dwie prace, w których autorzy badają stosowalność przybliżenia impulsowego i porównują tę metodę z całkowaniem numerycznym. Są to : praca Yabushita S., Hasegawa I., Kobayashi K., 1982, ( zwana dalej YHK ) oraz opublikowana kilka miesięcy później praca Scholl H., Cazenave A., Brachic A., 1982 ( zwana dalej SCB ).
ANALIZA WYNIKOW PRACY YABUSHITA, HASEGAWA, KOBAYASHI, 1982.
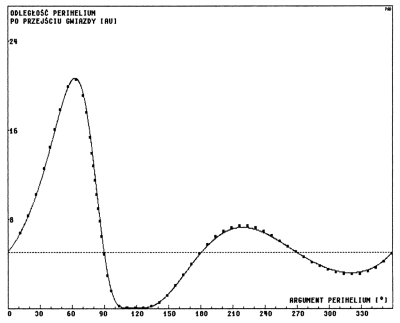
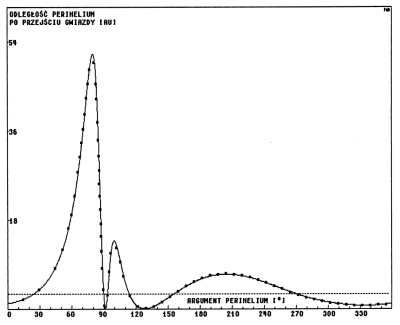
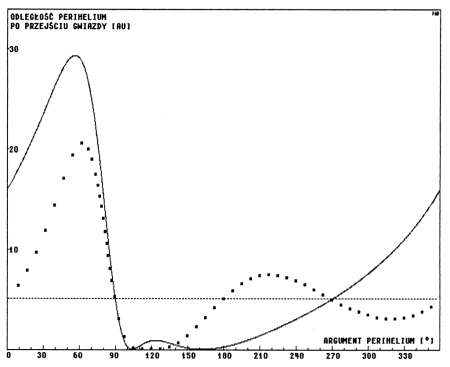
Rys.3.1. Metoda impulsowa a całkowanie numeryczne.
Por. Tab 1,str. 663 w pracy YHK
dla początkowego q∈ = 5.
W publikacji tej autorzy zajęli się wpływem perturbacji gwiazdowych na ruch komet długookresowych, których perihelia leżą już w obszarze obserwowalności ( q < 10 AU ). Jakkolwiek przedmiotem naszego zainteresowania są głównie komety o większych odległościach perihelium, to uzyskane w pracy YHK wyniki dotyczące stosowalności metody impulsowej są istotne i wymagają skomentowania.
Autorzy stosowali metodę impulsową w klasycznej postaci, uwzględniając różnicowy wpływ gwiazdy na kometę i Słońce.
Porównanie wyników całkowania numerycznego z wynikami otrzymanymi za pomocą przybliżenia impulsowego przeprowadzone zostało dla bardzo wąskiej klasy zagadnień. W przypadku orbity eliptycznej kometa była umieszczana zawsze dokładnie w aphelium. Rozważane były jedynie orbity leżące w płaszczyźnie wyznaczonej przez Słońce i tor gwiazdy lub prostopadłe do tej płaszczyzny. Prędkość gwiazdy we wszystkich rachunkach była równa 20 km/s. Masy gwiazdy nigdzie w pracy nie podano, jednak analiza otrzymanych wyników pokazuje, że była ona zawsze równa 1 Mo .
Dla całkowania numerycznego wybrano przedział czasu symetryczny względem momentu największego zbliżenia gwiazdy do Słońca i taki, by odległość kątowa pomiędzy początkową a końcową pozycją gwiazdy była równa 165° ( patrząc ze Słońca ). Pozwala to przypuszczać, że autorzy wzięli pod uwagę wyniki Rickmana (1976). Wprowadzony przez niego do metody impulsowej współczynnik ( por. wzory 2.3 ) jest dla tak wybranego przedziału całkowania równy 0.99 .
Stosując metodę impulsową w pełnej postaci otrzymaliśmy wyniki bardzo podobne do zamieszczonych w tabelach 1 i 3 omawianej pracy.
Wyniki powtórzonych rachunków, rozszerzonych do pełnego zakresu zmienności argumentu perihelium ilustrują wykresy na rysunkach 3.1 i 3.2 . Ciągła linia oznacza wyniki metody impulsowej, ciemne punkty natomiast wartości uzyskane z całkowania numerycznego.
Bardzo dobra zgodność obu metod wynika z kilku przyczyn. Przyjęta masa i prędkość gwiazdy oznacza stosunkowo słabe oddziaływa nie, szczególnie że gwiazda w rozważanych przypadkach przechodziła daleko od komety. Najmniejsza odległość wynosiła 10000 AU , w większości przypadków była jednak kilkakrotnie większa. Ponieważ długość całkowanego toru gwiazdy była niemal o rząd większa od odległości komety od Słońca, więc niesymetryczność przedziału czasu względem momentu zbliżenia gwiazdy do komety nie powodowała większych błędów. W trakcie obliczeń okazało się, że wartości podane w szóstej kolumnie tabeli 1 (YHK, str 663) zostały omyłkowo pomnożone przez 10.
Wyznaczając startową pozycję komety dla całkowania autorzy nie uwzględnili czasu,jaki potrzebuje gwiazda na przebycie połowy swej drogi ( do momentu największego zbliżenia do Słońca ) czyli kometa startowała dokładnie z aphelium. Słusznie uzasadniono takie postępowanie bardzo małą prędkością komety w aphelium tak wydłużonej orbity. W tabeli 4 (YHK, str 664) autorzy zamieszczają analogiczne do poprzednich porównanie przeprowadzone dla komety parabolicznej.
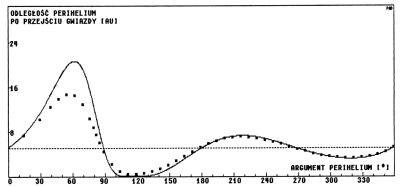
Gdyby również w tym przypadku ruch komety był całkowany od tego samego miejsca, dla którego stosowane są wzory metody impulsowej, wyniki odpowiadające tej tabeli wyglądałyby jak na rys 3.3 .
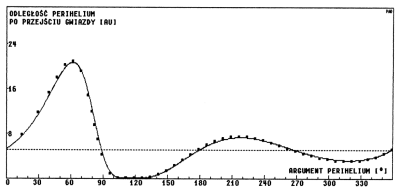
Rys.3.4. Metoda impulsowa a całkowanie numeryczne.
Por. tab 4,str. 664 w pracy YHK.
Dla argumentu perihelium mniejszego od 90° widać na tym wykresie znaczne różnice pomiędzy całkowaniem numerycznym a metodą impulsową. Aby wyeliminować przyczynę tak dużych błędów autorzy przed rozpoczęciem całkowania cofali kometę o 4000 AU wzdłuż jej parabolicznej orbity. Nawet tak prosty zabieg radykalnie poprawił zgodność wyników obu metod, co widać w cytowanej tabeli i w odpowiadającym jej wykresie przedstawionym na rysunku 3.4 .
W stosowanej w niniejszej pracy pełnej metodzie impulsowej opisane wyżej wyrównanie czasu realizowane jest dokładniej.
Po wyznaczeniu zmiany prędkości metodą impulsową kometa jest dla przeprowadzenia całkowania numerycznego cofana na orbicie niezaburzonej o czas DT . Czas ten wyznaczany jest z formuł nieperturbowanego, hiperbolicznego ruchu gwiazdy i odpowiada odcinkowi orbity gwiazdy od pozycji początkowej do punktu największego zbliżenia do komety ( a nie do Słońca jak w przypadku cytowanej pracy ).
Wyniki pracy YHK pokazują, że w rozpatrywanych przypadkach klasyczna metoda impulsowa daje wyniki zgodne z rezultatami całkowania numerycznego równań ruchu. Należy jednak jeszcze raz podkreślić, że autorzy tej pracy nie rozważali bliskich przejść gwiazdy obok komety, a porównanie przeprowadzali dla bardzo szczególnych konfiguracji, w których np. tor gwiazdy nigdy nie przecina orbity komety.
Zamieszczony w pracy YHK wniosek stwierdzający, że metoda impulsowa daje gorsze wyniki dla komet na orbitach parabolicznych jest zgodny z oczekiwaniem. Prędkość komety na takiej orbicie jest duża nawet na znacznej odległości od Słońca, co wyraźnie narusza jedno z założeń przyjętych przy wyprowadzaniu metody impulsowej.
Ważnym rezultatem omawianej pracy jest też wniosek, że gwiazda o masie równej 1 Mo,mająca stosunkowo dużą prędkość i przechodząca w odległości kilkudziesięciu tysięcy jednostek astronomicznych od komety może znacząco zmienić jej orbitę, np. zmienić kierunek ruchu z prostego na wsteczny. Pewne uwagi do statystycznej części pracy YHK sformułujemy w rozdziale piątym.
KRYTYKA PRACY SCHOLL, CAZENAVE, BRAHIC, 1982.
Autorzy tej pracy podjęli próbę nakreślenia całościowego obrazu wpływu perturbacji gwiazdowych na ruch komet w obłoku Oorta.
We wstępie sformułowali cztery cele :
- wyznaczenie ilościowych zależności zmian orbit kometarnych od parametrów problemu, mianowicie geometrii zbliżenia, masy gwiazdy, najmniejszej odległości gwiazdy od komety itd.;
- znalezienie szczególnych konfiguracji, prowadzących do redukcji odległości perihelium komety poniżej granicy obserwowalności;
- rozważenie możliwości identyfikacji rodzin komet wprowadzonych do sfery obserwowalności przez tę samą gwiazdę;
- testowanie zakresu stosowalności Maxwell'owskiego rozkładu przyrostów prędkości, proponowanego przez Oorta i Weissmana (1980) do uproszczonych badań statystycznych.
Uważna lektura pracy SCB prowadzi do wniosku, że ani jeden z wymienionych celów nie został w pełni zrealizowany.
Zależność zmian elementów orbity komety od parametrów zagadnienia rozważono, wbrew wstępnym zapowiedziom, na bardzo ograniczonej próbie. Przedstawiono wyniki tylko dla przejść gwiazd poza orbitą komety, tor gwiazdy był zawsze prostopadły do linii węzłów, kometa pozostawała zawsze w bezpośrednim sąsiedztwie węzła wstępującego, który prawie we wszystkich przypadkach pokrywał się z aphelium orbity komety. Klasa przypadków, dla których podano wyniki, jest więc niewiele większa od zakresu rozpatrywanego w pracy YHK.
Nie został przedstawiony ani jeden przypadek zmniejszenia odległości perihelium komety poniżej granicy obserwowalności. Wniosek, że taka zmiana wymaga orbity prawie prostopadłej do płaszczyzny ruchu gwiazdy i minimalnej odległości od komety poniżej 2000 AU jest słabo uzasadniony, co potwierdza kilka przykładów zamieszczonych w następnym rozdziale.
Problem identyfikacji gwiazdy, odpowiedzialnej za powstanie konkretnej, obserwowalnej komety długookresowej uznano za trudny i wciąż otwarty.
Czwarte z wymienionych zagadnień nie jest w pracy dyskutowane. Dużo miejsca w pracy SCB poświęcono porównaniu całkowania numerycznego pełnego zagadnienia trzech ciał z dwoma metodami uproszczonymi. Pierwsza z nich to całkowanie numeryczne, w którym zaniedbuje się wpływ gwiazdy na Słońce; druga to przybliżenie impulsowe również z zaniedbaniem efektu różnicowego.
Końcowy wniosek z tych porównań, stwierdzający dobrą zgodność wyników i tym samym uznający za zaniedbywalny wpływ gwiazdy na Słońce nie jest prawdziwy. Jego potwierdzenie rezultatami obliczeń wynika tylko ze szczególnego doboru danych, co pokażemy niżej. Autorzy posługiwali się w rozważaniach układem odniesienia identycznym z opisanym w poprzednim rozdziale układem OXYZ. Linia węzłów orbity kometarnej pokrywała się we wszystkich przypadkach z osią OY. Kometa umieszczana była zawsze w bezpośrednim otoczeniu węzła wstępującego, czyli blisko płaszczyzny ruchu gwiazdy. Zatem we wszystkich przypadkach w momencie największego zbliżenia gwiazdy do Słońca, który prawie pokrywał się z momentem największego zbliżenia do komety, wszystkie trzy ciała: Słońce,kometa i gwiazda znajdowały się niemal w jednej linii. Tor gwiazdy przebiegał zawsze na zewnątrz orbity komety blisko jej węzła wstępującego.
W tabeli 4 na str 164 w pracy SCB podano zmianę odległości perihelium i aphelium komety po przejściu gwiazdy, uzyskane z całkowania numerycznego pełnego zagadnienia.
Stosowane przez nas metody całkowania dały wyniki całkowicie zgodne.
W cytowanej tabeli (SCB, str 164) podano też najmniejszą odległość gwiazdy od komety. Odległość ta waha się od 2000 do 9000 AU. Jest ona za duża, by zaobserwować opisany w poprzednim rozdziale i dyskutowany dalej efekt zakrzywienia kometocentrycznego toru gwiazdy. Jest ona jednak na tyle mała w porównaniu z przyjętą odległością komety od Słońca ( 100000 AU ), by wobec współliniowości Słońca, komety i gwiazdy można było uznać wpływ gwiazdy na Słońce za nieistotny.
Jeszcze raz podkreślmy, że zaniedbanie zmiany prędkości Słońca pod wpływem przechodzącej gwiazdy, tak w całkowaniu numerycznym jak i w metodzie impulsowej, było w pracy SCB możliwe tylko dzięki szczególnemu określeniu geometrii zbliżenia.
W tabeli 6 omawianej pracy (SCB,str.166 ) zamieszczono uzyskane przez autorów różnice pomiędzy rezultatami całkowania numerycznego pełnego zagadnienia a wynikami metody impulsowej, w której zaniedbano zmianę prędkości Słońca. Ścisłe powtórzenie tych rachunków nie było możliwe, ponieważ autorzy nie podali jak wyznaczali najbliższy toru gwiazdy punkt orbity komety,w którym stosowali metodę impulsową. Duży rozrzut błędu wyrażonego w procentach ( od zera do 11%) wynika z faktu,iż wpływ błędu wyznaczonej zmiany prędkości komety na zmianę jej odległości perihelium jest zależny nie tylko od elementów orbity komety lecz również, a nawet głównie, od konfiguracji geometrycznej w chwili największego zbliżenia.
Potwierdzeniem tego wniosku mogą być wyniki przytoczone w zamieszczonej poniżej Tabeli 1. Zawiera ona różnice pomiędzy całkowaniem numerycznym a metodą impulsową z uwzględnieniem efektu różnicowego, dla wszystkich przykładów z tabeli 6 pracy SCB.
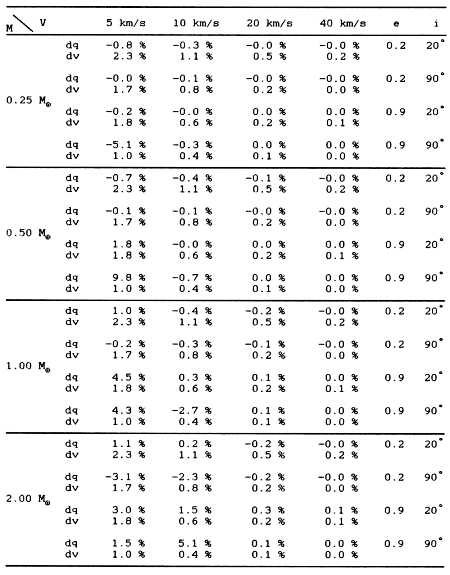
Tabela 1. Różnice pomiędzy metodą impulsową
a całkowaniem numerycznym. Por. Tab.6 w pracy SCB, str 166.
Oprócz procentowego błędu w odległości perihelium zamieściliśmy procentowy błąd wyznaczenia zmiany prędkości. Jest to stosunek długości różnicy wektorów przyrostu prędkości, uzyskanych obydwoma metodami, do długości wektora przyrostu prędkości otrzymanego z całkowania numerycznego. W czasie wyliczania tego ostatniego błędu był on mnożony przez minus jeden, gdy moduł wektora zmiany prędkości, wyliczony metodą impulsową był większy od modułu wektora otrzymanego z całkowania. Brak ujemnych wartości dv w tabeli 1 wskazuje, że we wszystkich przypadkach przyrost prędkości uzyskany z całkowania numerycznego był większy od uzyskanego metodą impulsową.
Zamieszczone w Tab.1. wartości pokazują też, że procentowy błąd wyznaczenia wektora zmiany prędkości komety nie zależy od masy gwiazdy, natomiast silnie zależy od jej prędkości. Uwzględnienie w metodzie impulsowej wpływu gwiazdy na prędkość Słońca zmniejszyło w wielu przypadkach błąd wyznaczenia odległości perihelium, mimo iż autorzy minimalizowali ten efekt poprzez opisany wyżej dobór danych wyjściowych.
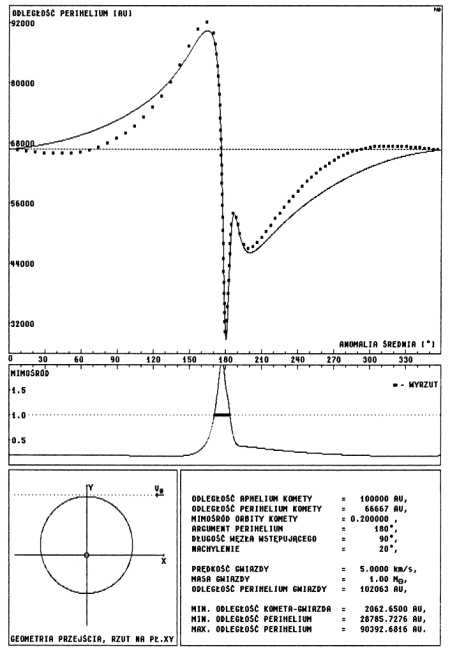
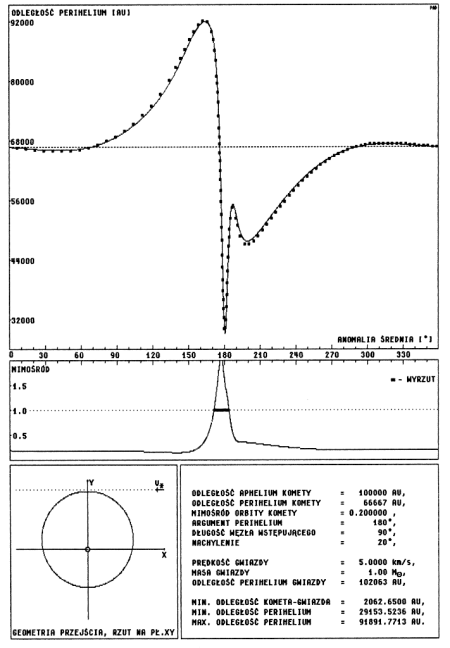
Przeanalizujmy dla przykładu przypadek, w którym w tabeli 6 pracy SCB pojawia się największy błąd bezwzględny, równy 3300 AU. Występuje on, gdy M = 1 Mo, V = 5 km/s, e = 0.2 oraz i = 20° i odpowiada mu błąd procentowy równy 5.9% . Jak widać w Tabeli 1 uwzględnienie zmiany prędkości Słońca prowadzi do sześciokrotnego zmniejszenia różnicy pomiędzy wynikiem całkowania a odległością perihelium wyznaczoną metodą impulsową. Przyjęty w pracy SCB sposób przeprowadzenia rachunków powodował, że dla niedużych mimośrodów punkt największego zbliżenia komety z gwiazdą wypadał wbrew intencji autorów wyraźnie po aphelium. W analizowanym przypadku anomalia średnia punktu największego zbliżenia wynosiła ok. 190° . Poza aphelium efekt różnicowy zaczyna być widoczny, co widać gdy porównamy wykresy przedstawione na rysunkach 3.5 i 3.6 zamieszczonych poniżej. Wykresy te różnią się tylko tym, że w pierwszym przypadku nie uwzględniliśmy wpływu gwiazdy na Słońce !
Ponieważ taka forma rysunku będzie przez nas stosowana częściej, opiszemy ją w tym miejscu dokładniej. Główny wykres przedstawia zależność odległości perihelium komety po przejściu gwiazdy od anomalii średniej, opisującej pozycję komety na niezaburzonej orbicie w momencie największego zbliżenia z gwiazdą. Linia ciągła oznacza wyniki uzyskane metodą impulsową, ciemne punkty wskazują wartości uzyskane z całkowania numerycznego. Pozioma, przerywana linia, oznacza początkową wartość odległości perihelium komety.
Poniżej, oparty o tę samą skalę anomalii średniej, pokazany jest wykres zmian mimośrodu komety. Kropkowana linia oznacza mimośród równy jedności. Dla mimośrodów większych od jedności na tej kropkowanej linii oznaczane są ciemną, grubą linią przedziały, w których kometa po przejściu gwiazdy znajduje się w takim miejscu orbity hiperbolicznej, że nigdy nie przejdzie przez perihelium.
W takich przedziałach kometa nie może być zaobserwowana nawet gdy odległość perihelium jest mniejsza od granicy obserwowalności. W lewej, dolnej części każdego rysunku zamieszczony jest szkic konfiguracji geometrycznej przejścia gwiazdy. Jest to rzut na płaszczyznę XY lub YZ, zależnie od nachylenia orbity. Obok wypisane są najważniejsze parametry zagadnienia. Trzy ostatnie wartości odnoszą się do metody impulsowej.
Dla innych, przypadkowych konfiguracji błędy wynikające z pominięcia efektu różnicowego są zwykle znacznie większe. Na przykład wykres zamieszczony na rys. 3.1 po zaniedbaniu tego efektu wyglądałby jak na rys.3.7.
Inny układ odniesienia, stosowany w pracy YHK powoduje, że konfiguracjom geometrycznym wybieranym do rachunków testowych w pracy SCB odpowiada tu otoczenie punktu o anomalii średniej 90° .
Na rysunku 3.7 widać, że tylko w bezpośrednim sąsiedztwie tej wartości całkowanie numeryczne daje wyniki zgodne z metodą impulsową nieuwzględniającą zmiany prędkości Słońca.
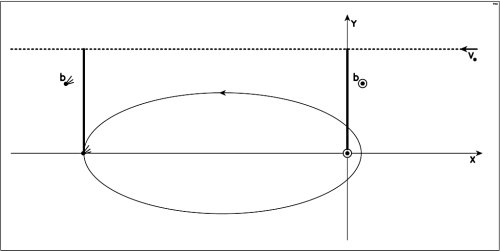
Aby ostatecznie przekonać się o konieczności uwzględniania zmiany prędkości Słońca w metodzie impulsowej rozważmy następujące (dla uproszczenia płaskie) zagadnienie:w jakim przypadku przejście gwiazdy spowoduje największą zmianę odległości perihelium komety na orbicie eliptycznej jeśli zaniedbamy efekt różnicowy.
Proste rozważanie prowadzi do odpowiedzi, że należy kometę umieścić w aphelium, gdzie ma najmniejszą prędkość orbitalną , a orbitę zorientować tak, by tor gwiazdy był równoległy do linii absyd. Kierunek impulsu prędkości pochodzącego od gwiazdy jest wtedy zgodny z kierunkiem prędkości orbitalnej. Przykład takiej konfiguracji w płaszczyźnie OXY przedstawia rys. 3.8.
Łatwo natomiast zauważyć, że gdy uwzględnimy zmianę prędkości Słońca, to całkowity wpływ gwiazdy wyznaczany metodą impulsową będzie równy zeru, niezależnie od odległości toru gwiazdy od komety czy Słońca.
Jeżeli więc wyznaczamy zmianę orbity komety w przypadkowych konfiguracjach ( np. w symulacyjnych badaniach większych populacji komet ) zaniedbanie efektu różnicowego jest niedopuszczalne.
METODA IMPULSOWA: WERSJA KLASYCZNA CZY PEŁNA?
Wyprowadzona w poprzednim rozdziale pełna postać przybliżenia impulsowego w stosunku do wersji klasycznej uwzględnia dwa dodatkowe zjawiska. Po pierwsze niesymetryczność przedziału czasu w stosunku do momentu największego zbliżenia gwiazdy do komety i Słońca, po drugie wpływ zakrzywienia heliocentrycznego i kometocentrycznego toru gwiazdy na kierunek i długość wektora przyrostu heliocentrycznej prędkości komety.
Uwzględnienie pierwszego efektu jest szczególnie istotne, gdy porównujemy wyniki metody impulsowej z rezultatami całkowania numerycznego, realizowanego na skończonym przedziale czasu.
Najczęściej wybierany jest przedział symetryczny względem momentu największego zbliżenia gwiazdy do Słońca, tak więc efekt ten jest zauważalny tylko w oddziaływaniu gwiazdy na kometę. Jak pokazano w Dodatku, niesymetryczność ta powoduje z jednej strony zmianę długości wektora przyrostu prędkości komety, z drugiej zaś strony zmianę kierunku tego wektora tak, że zawsze jest on skierowany wzdłuż dwusiecznej kąta utworzonego przez początkowy i końcowy, kometocentryczny wektor wodzący gwiazdy.
Ze wzoru (D.4) wynika, że jeśli przyrost kometocentrycznej anomalii prawdziwej gwiazdy na odcinku orbity, z którego uwzględniamy oddziaływanie, jest dostatecznie bliski 180° , to moduł wektora zmiany prędkości komety jest wystarczająco dokładnie opisany wzorami klasycznej metody impulsowej. Jeśli tak nie jest, to wynik metody klasycznej należy pomnożyć przez sinus połowy przyrostu tej anomalii.
Ze wzorów (D.3) wynika, że wektor przyrostu prędkości jest skierowany pod kątem (ϑ1 + ϑ2 )/2 do linii absyd kometocentrycznej orbity gwiazdy.Przez ϑ1 i ϑ2 oznaczyliśmy tu początkową i końcową, kometocentryczną anomalię prawdziwą gwiazdy. Skręcenie to można zaniedbać tylko wtedy, gdy obie wartości anomalii są bliskie co do modułu i różnią się znakami.
Jeżeli wycinek orbity gwiazdy jest również niesymetryczny względem punktu najbliższego Słońcu, to powyższe uwagi odnoszą się również odpowiednio do wyznaczania członu słonecznego.
Metodę impulsową najczęściej jednak stosuje się do wyznaczania zmiany orbity komety pod wpływem oddziaływania gwiazdy uwzględniając cały tor gwiazdy. Nie występuje wtedy zmiana kierunku impulsu prędkości wynikająca z niesymetryczności wycinka hiperboli gwiazdowej. Całkowity przyrost anomalii prawdziwej gwiazdy względem komety i Słońca jest jednak wtedy zawsze większy od 180° i to tym wyraźniej, im bardziej zakrzywiony jest heliocentryczny bądź kometocentryczny tor gwiazdy. Efekt ten jest uwzględniony we wzorach (2.6) pełnej metody impulsowej dla nieskończonego przedziału czasu oddziaływania.
Wzory te, podobnie jak ich pełna wersja (2.5) dla dowolnego przedziału czasu, uwzględniają też drugie ze wspomnianych wyżej zjawisk, pomijanych w metodzie klasycznej. Chodzi tu o wpływ zakrzywienia heliocentrycznego i kometocentrycznego toru gwiazdy na kierunek i długość wektora zmiany prędkości. Jak pokażemy niżej wpływ ten nie może być pominięty dla bliskich przejść gwiazdy obok komety lub Słońca.
Wzory (2.7) metody klasycznej, jak już zauważyliśmy pomijają składową ΔVx zmiany prędkości komety, natomiast w pozostałych składowych człony kometarne różnią się o czynnik c∈2/ b∈2 , a człony słoneczne o czynnik co2/ bo2 .
Problem pomijalności składowej ΔVx można tu rozstrzygnąć badając oddzielnie wielkość członu kometarnego i słonecznego w tej składowej i rozważając wartości poniższych stosunków:
(3.1)
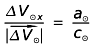
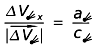
W obu przypadkach skorzystać możemy ze związku :
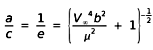
w którym przez e oznaczyliśmy mimośród orbity.
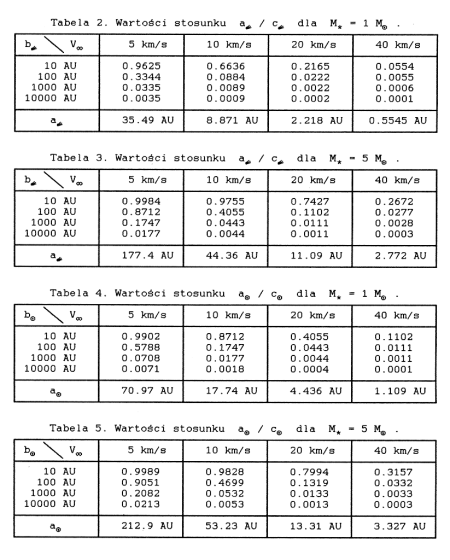
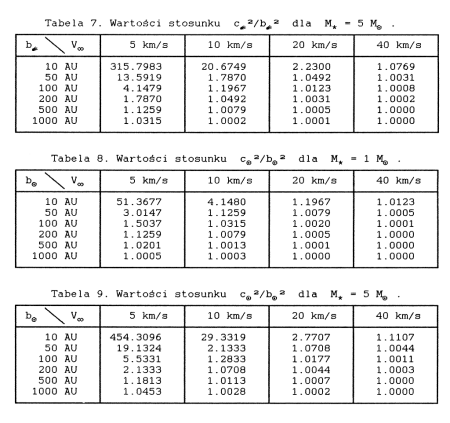
Poniższe tabele zawierają wartości tego stosunku dla dwóch różnych wartości masy gwiazdy w zależności od jej prędkości i małej półosi, oddzielnie dla komety i Słońca.
W ostatnim wierszu każdej tabeli zamieszczono dodatkowo wartość wielkiej półosi odpowiadającą danej masie i prędkości gwiazdy.
Nawet pobieżna analiza powyższych tabel pokazuje, że dla bliskich przejść gwiazdy obok komety lub Słońca składowa równoległa do osi OX jest znacząca, a dla przejść bardzo ciasnych, wręcz dominująca. Jeżeli np. gwiazda o masie 5 Mo i prędkości 5 km/s przechodzi 1000 AU od komety, to składowa ta wynosi 17 % modułu całkowitego przyrostu prędkości komety ( tab. 3 ).
Jak wynika z zależności (3.1) klasyczna metoda impulsowa daje prawidłowe wyniki tylko wtedy, gdy wartości omawianych wyżej stosunków są bliskie zeru.
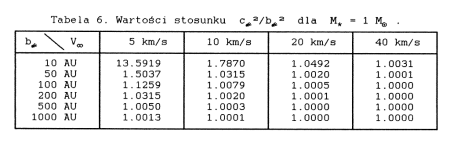
Aby przedyskutować różnicę pomiędzy klasyczną i pełną metodą impulsową w pozostałych dwóch składowych wektora zmiany prędkości komety, wyliczymy poniżej wartości współczynnika c2/b2 , o który różnią się wzory obu tych metod. Korzystając z formuł nieperturbowanego zagadnienia dwóch ciał możemy ten współczynnik, podobnie jak poprzednio, wyliczyć z danych początkowych ruchu gwiazdy:
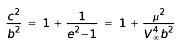
Tabele 6 do 9 zawierają wartości tego współczynnika dla różnych mas gwiazdy, oddzielnie dla komety i Słońca. Potwierdzają one w pełni sformułowaną wcześniej tezę, że stosowanie przybliżenia impulsowego w klasycznej postaci do przypadków bliskich przejść gwiazdy obok komety lub Słońca prowadzić może do znaczących, a niekiedy dużych błędów.
Metoda klasyczna daje wynik zgodny z wersją pełną tylko wtedy,gdy powyższe współczynniki są równe jedności.
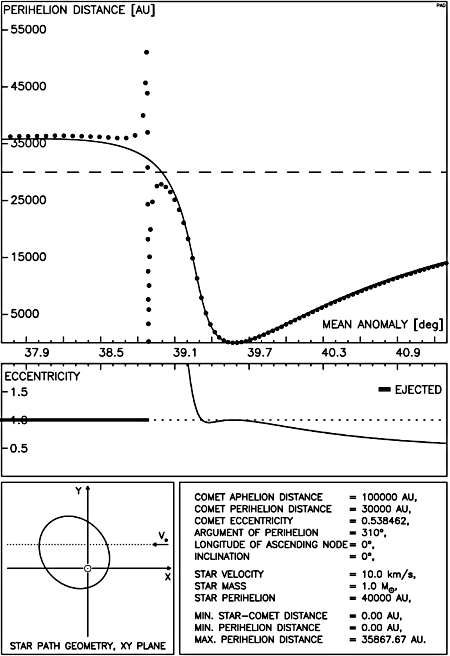
Rys.3.9. Klasyczna metoda impulsowa
a całkowanie numeryczne.PS
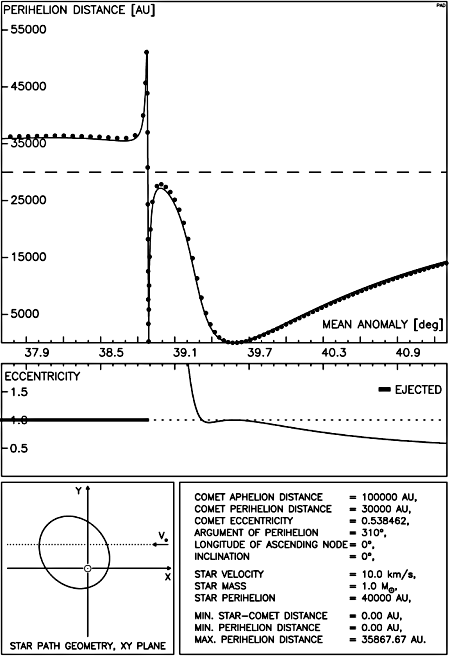
Rys.3.10. Pełna metoda impulsowa
a całkowanie numeryczne.PS
Na koniec pokażemy konieczność stosowania pełnej formy przybliżenia impulsowego na konkretnym przykładzie bliskiego przejścia gwiazdy obok komety. Rysunki 3.9 i 3.10 przedstawiają w opisanej już postaci zależność końcowej odległości perihelium komety od jej anomalii średniej.
W rozważanym przypadku orbita komety leży w płaszczyźnie ruchu gwiazdy i jest przez jej tor przecinana. Minimalna odległość gwiazdy od komety jest w tym przypadku dowolnie mała.
Na obu rysunkach przedstawiamy otoczenie tego samego punktu przecięcia orbity komety przez tor gwiazdy. Punktowi temu odpowiada anomalia średnia komety równa ok. 38.8° .
Na Rysunku 3.9 prezentujemy wyniki całkowania numerycznego ( ciemne punkty ) i klasycznej metody impulsowej z uwzględnieniem efektu różnicowego ( linia ciągła ). Wyraźnie widać, że metoda klasyczna daje całkowicie błędny przebieg zmian odległości perihelium komety w otoczeniu punktu przecięcia z torem gwiazdy.
Rysunek 3.10 przedstawia ten sam przebieg, metoda klasyczna została jednak zastąpiona pełną wersją. Na tym rysunku oba przebiegi prawie się pokrywają. Trzeba jednak zaznaczyć, że gdy porównamy konkretne wartości numeryczne, uzyskane pełną metodą impulsową i całkowaniem numerycznym w bezpośrednim otoczeniu punktu przecięcia orbity komety z torem gwiazdy, to otrzymane różnice mogą być duże. Zarówno błąd samego przybliżenia impulsowego jak i nie dokładności w danych startowych dla całkowania przejawiają się na tych wykresach niewielkimi, poziomymi przesunięciami przebiegów. Na pionowych odcinkach wykresów powoduje to często znaczne różnice ilościowe pomimo dobrej zgodności jakościowej.
Efekt pokazany na rysunkach 3.9 i 3.10 występuje zawsze, gdy tor gwiazdy przecina orbitę komety lub gdy przechodzi blisko niej, niekoniecznie w tej samej płaszczyźnie. Jest on niezależny od elementów orbity komety oraz parametrów ruchu gwiazdy lub jej masy.
W następnym rozdziale pokażemy szczegółowo jak zmienia się odległość perihelium komety pod wpływem oddziaływania przechodzącej gwiazdy. We wszystkich przypadkach, w których przedstawiać będziemy wykresy szczegółowe stosowana będzie pełna metoda impulsowa jednocześnie z całkowaniem numerycznym.
Wyniki rozdziału czwartego są zatem jednocześnie uzupełnieniem niniejszych rozważań o stosowalności przybliżenia impulsowego, stanowią bowiem obszerne porównanie wyników przybliżonych z całkowaniem numerycznym, przeprowadzone dla różnych wartości wszystkich parametrów zagadnienia, mieszczących się w przedziałach wskazanych w rozdziale drugim.