II. METODY WYZNACZANIA PERTURBACJI GWIAZDOWYCH W RUCHU KOMET.
Zagadnienie wpływu bliskiego przejścia gwiazdy na ruch komety będziemy rozważać w prostokątnym, prawoskrętnym, heliocentrycznym układzie współrzędnych. Do opisu orbit będziemy używać tradycyjnego zestawu elementów. Rozmiar i kształt orbity określają tu: odległość perihelium q oraz mimośród e , orientację orbity względem układu odniesienia definiują natomiast: długość węzła wstępującego Ω , argument perihelium ω oraz nachylenie orbity i .
Pozycję ciała na orbicie opisywać będzie moment czasu albo wartość anomalii średniej lub prawdziwej . W rachunkach i tabelach będziemy też posługiwać się odległością aphelium Q oraz wielką półosią orbity a . Hiperboliczną orbitę gwiazdy będziemy też opisywać podając zamiast elementów q oraz e wektor prędkości gwiazdy w nieskończoności V∞ ,odległość asymptoty zawierającej ten wektor od środka układu b i masę gwiazdy M∗.
Wszystkie odległości podawane będą w jednostkach astronomicznych ( AU ), jednostką masy będzie masa Słońca Mo, jednostką czasu doba. Jedynie prędkość gwiazdy podawać będziemy tradycyjnie w kilometrach na sekundę.
Ponieważ niektóre z opisywanych dalej metod są metodami przybliżonymi, należy więc na wstępie podać również zakres wartości niektórych parametrów opisujących zagadnienie, aby móc dyskutować stosowalność przyjętych uproszczeń. I tak : rozważane prędkości gwiazd mieszczą się w przedziale od 5 do 40 km/s, odległości periheliów gwiazd od 1·104 do 1·105 AU, masy gwiazd od 0.5 do 5 Mo.
W rozważaniach brane będą pod uwagę wszystkie orbity komet, mieszczące się w sferze o promieniu 1.2·105 AU, ze środkiem w Słońcu, pomijać będziemy jednak wpływ układu planetarnego na te orbity. Masa komety będzie każdorazowo przyjmowana jako równa zeru. Podane wyżej przedziały wartości parametrów są w większości dotychczasowych publikacji określane jako typowe.
Jedyną metodą wyznaczania zmian orbity komety pod wpływem przechodzącej gwiazdy, dającą wyniki z dokładnością ograniczoną tylko długością słowa maszynowego zastosowanego komputera oraz dostępnym czasem obliczeń, jest całkowanie numeryczne równań różniczkowych ruchu. Jednak duża czasochłonność takich obliczeń skłania wielu autorów do stosowania metody przybliżonej, zwanej metodą impulsową lub przybliżeniem impulsowym.
METODA IMPULSOWA POSTAĆ KLASYCZNA.
Oort (1950) formułując hipotezę o istnieniu obłoku kometarnego zaproponował za Öpikiem (1932) wyznaczanie perturbacji gwiazdowych w ruchu komet z tego obłoku przy pomocy przybliżenia impulsowego.
Oort stwierdził, jawnie nie formułując warunków stosowania tego przybliżenia, że całkowity efekt grawitacyjnego oddziaływania gwiazdy na kometę można z wystarczającą dokładnością uzyskać dodając do prędkości komety w momencie jej największego zbliżenia do gwiazdy impulsową zmianę prędkości, wyrażoną wzorem:
(2.1)
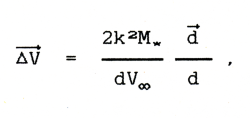
gdzie d jest wektorem poprowadzonym od komety, pozostającej na nieperturbowanej orbicie, do gwiazdy w momencie ich największego zbliżenia. Ponieważ trzeba uwzględnić analogiczną impulsową zmianę prędkości Słońca, ostateczny wzór przyjmie postać:
(2.2)
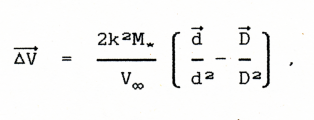
w której D jest wektorem poprowadzonym ze Słońca do gwiazdy w momencie ich największego zbliżenia. Oort w swojej pracy założył, że punkty największego zbliżenia gwiazdy do Słońca i do komety pokrywają się. W dodatku do pracy potwierdził uwagę recenzenta, że takie założenie na ogół nie jest spełnione i zaproponował jako rozwiązanie tej trudności pomijanie wpływu gwiazdy na Słońce lub kometę w zależności od geometrii przejścia.
Rickman (1976) wyprowadził wzory dla przybliżenia impulsowego wychodząc z równań ruchu w zagadnieniu trzech ciał, które scałkował analitycznie, formułując jawnie (w przeciwieństwie do Oorta) trzy istotne uproszczenia będące podstawą metody impulsowej w klasycznej postaci:
- r∈ = const, co oznacza, że kometa pozostaje w spoczynku podczas przejścia gwiazdy. Jest to równoważne "zamrożeniu" na czas tego przejścia oddziaływania kometa Słońce oraz zaniedbaniu przemieszczenia komety na skutek oddziaływania z gwiazdą;
- przedział czasu, w którym rozważamy oddziaływanie gwiazdy jest na tyle duży, że można traktować go jako symetryczny tak względem momentu największego zbliżenia gwiazdy z kometą jak i największego zbliżenia ze Słońcem;
- V* = const = V∞, co oznacza, że tor gwiazdy jest linią prostą, a gwiazda porusza się ruchem jednostajnym. Jest to równoważne zaniedbaniu wpływu Słońca na ruch gwiazdy.
Całkując jednokrotnie równania ruchu na przedziale czasu <-T,T> Rickman otrzymał następujące wzory na zmianę prędkości komety i Słońca :
(2.3)
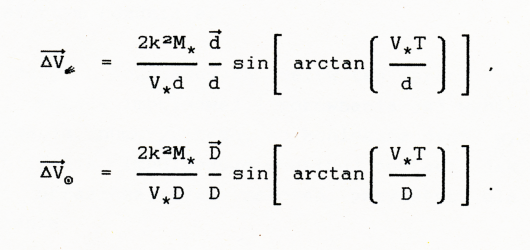
W porównaniu do poprzednich wzory te zawierają na końcu pewien współczynnik. Jest to sinus połowy kąta, pod jakim ze Słońca widać drogę przebytą przez gwiazdę w czasie od -T do T . Rickman zaznacza jednak, że przy dostatecznie dużym T współczynnik ten można pominąć jako równy jedności, co też czynią wszyscy inni autorzy.
Metoda impulsowa w klasycznej postaci była i jest nadal używana przez wielu autorów, np.: Sekanina, 1968; Bailey, 1983a, 1986a; Weissman, 1980, 1982, 1983; Fernandez, 1980, 1981; Scholl i inni, 1982; Yabushita i inni,1982; Remy i Mignard, 1985; Mignard i Remy, 1985; Rickmann i Froeschle, 1988.
Dopiero ostatnio w pracy Morrisa i O'Neilla (1988) pojawiła się pierwsza, ograniczona próba uwzględnienia wzajemnego oddziaływania gwiazdy ze Słońcem. Autorzy tej pracy zauważają bowiem, że nawet dla T =∞ współczynnik, o który Rickman rozszerzył wzory metody impulsowej, nie jest równy jedności, gdy uwzględni się zakrzywienie toru gwiazdy.
W cytowanej pracy Rickmana jest ukryte jeszcze jedno założenie, niezbędne dla otrzymania podanego wyżej wyniku. Rickman zakłada mianowicie, że podobnie jak wektor zmiany prędkości Słońca również wektor zmiany prędkości komety jest prostopadły do toru gwiazdy, który u Rickmana jest linią prostą.
Jak pokażemy dalej takie założenie jest równoważne stwierdzeniu, że nie tylko heliocentryczna ale również kometocentryczna orbita gwiazdy jest linią prostą. Jest to prawdą tylko wtedy, gdy gwiazda przechodzi dostatecznie daleko od komety. Dokładniej rozważymy ten problem w następnym rozdziale.
Ponieważ jednym z podstawowych celów tej pracy jest analiza stosowalności metody impulsowej i porównanie jej wyników z rezultatami całkowania numerycznego, to konieczne jest wyprowadzenie wzorów przybliżenia impulsowego w pełnej postaci jak też ścisłe sformułowanie upraszczających założeń, przyjętych dla otrzymania tego przybliżenia.
Poniżej pokażemy, że ogólniejsze i bardziej dokładne wzory metody impulsowej można łatwo wyprowadzić, odrzucając nie tylko to "ukryte", ale też część jawnie sformułowanych u Rickmana założeń.
METODA IMPULSOWA POSTAĆ PEŁNA.
Istotą przybliżenia impulsowego jest rozdzielenie zagadnienia trzech ciał: Słońce-gwiazda-kometa na dwa niezależne zagadnienia dwóch ciał: gwiazda-Słońce oraz gwiazda-kometa. Oddzielnie wyznaczane są barycentryczne wektory zmiany prędkości komety i Słońca w odpowiednich układach inercjalnych. Zmianę prędkości komety względem Słońca uzyskuje się jako różnicę tych wektorów po ich przetransformowaniu do wspólnego układu odniesienia.
Jedyne dwa uproszczenia jakie wynikają z takiego sformułowania metody to założenie, że kometa nie zmienia pozycji podczas przejścia gwiazdy, czyli nie ma oddziaływania komety ze Słońcem a gwiazda powoduje jedynie zmianę prędkości komety oraz założenie,że zakrzywienie toru gwiazdy przez Słońce nie ma wpływu na oddziaływanie gwiazdy na kometę.
Wektor przyrostu prędkości jednego ciała w pewnym interwale czasu <t1 ,t2 >, wynikający z oddziaływania grawitacyjnego drugiego ciała w hiperbolicznym zagadnieniu dwóch ciał można wyznaczyć dokładnie ( patrz Dodatek ). Wprawdzie symetria przedziału czasu względem momentu przejścia perycentrum upraszcza końcowe wzory, nie jest jednak konieczna do otrzymania wyniku. Również założenie o prostoliniowym ruchu gwiazdy, a w rzeczywistości również o prostopadłości wektora zmiany prędkości komety i Słońca do toru gwiazdy jest niepotrzebne i, jak to pokażemy dalej, może prowadzić w pewnych przypadkach do istotnych błędów. Ma to szczególne znaczenie, gdy gwiazda przechodzi blisko Słońca lub komety. Wprawdzie w niniejszej pracy, jak też w większości dotychczasowych prac, wyklucza się bardzo bliskie przejście gwiazdy obok Słońca (przemawiają za tym zarówno argumenty statystyczne jak i dynamiczne ), to jednak na wartość najmniejszej odległości gwiazdy od komety nie wprowadza się, co oczywiste, żadnych ograniczeń.
Heliocentryczny układ współrzędnych OXYZ , w którym wyznaczymy wektor zmiany prędkości komety pod wpływem przejścia gwiazdy zorientowany jest tak, że płaszczyzna OXY pokrywa się z płaszczyzną ruchu gwiazdy a oś OX jest równoległa do wektora początkowej prędkości V∞ gwiazdy względem Słońca lecz przeciwnie skierowana.
Oś OZ jest zgodna z wektorem momentu pędu gwiazdy, oś OY zaś tworzy z pozostałymi układ prawoskrętny. Pozycję komety w tym układzie opisuje wektor r∈ = (x∈ ,y∈ ,z∈ ) , odległość asymptoty orbity gwiazdy, zawierającej wektor V∞ od środka układu (czyli Słońca) oznaczymy przez bo , natomiast masę gwiazdy przez M* .
Heliocentryczna orbita gwiazdy jest dana, półoś mała tej orbity jest równa bo , a znając prędkość V∞ możemy łatwo wyznaczyć półoś wielką:

Ponieważ zgodnie z przyjętym założeniem w czasie przelotu gwiazdy r∈ = const, więc dana jest też jej kometocentryczna orbita:
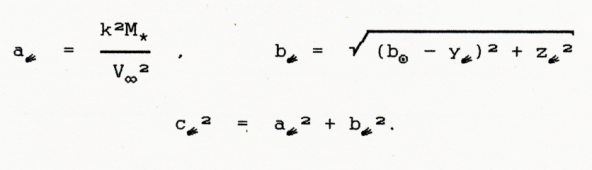
Mając te dane, barycentryczne zmiany prędkości komety i Słońca w pewnym, wspólnym przedziale czasu <t ,t >,otrzymamy bezpośrednio ze wzorów (D.12) i (D.13) wyprowadzonych w dodatku do tej pracy.
Wystarczy w tym celu podstawić do nich parametry kometocentrycznej a następnie heliocentrycznej orbity gwiazdy. Ponieważ płaszczyzna kometocentrycznego toru gwiazdy jest nachylona pod pewnym kątem β do płaszczyzny toru heliocentrycznego więc wyznaczenie różnicy otrzymanych wektorów wymaga dokonania odpowiedniej transformacji. Z geometrii zagadnienia w układzie OXYZ wynika, że:

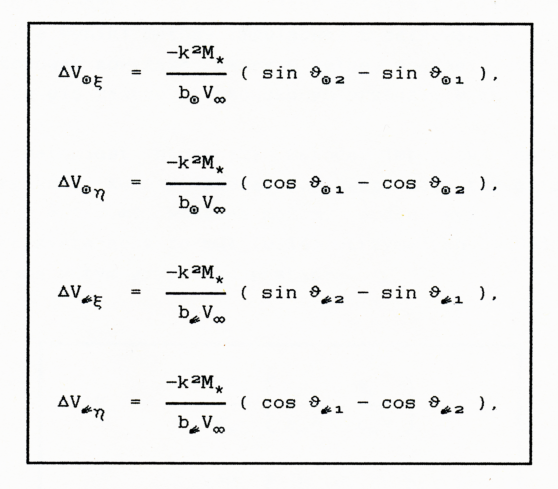
Ze wzorów (D.12) otrzymamy składowe zmian prędkości w układach orbitalnych: ΔVoξ , ΔVoη, ΔV∈ξ i ΔV∈η. Po podstawieniu tych składowych do wzorów (D.13) i dokonaniu odpowiednich przekształceń i transformacji, uzyskamy szukane składowe wektora ΔV zmiany prędkości komety względem Słońca w układzie OXYZ.
(2.4)
(2.5)
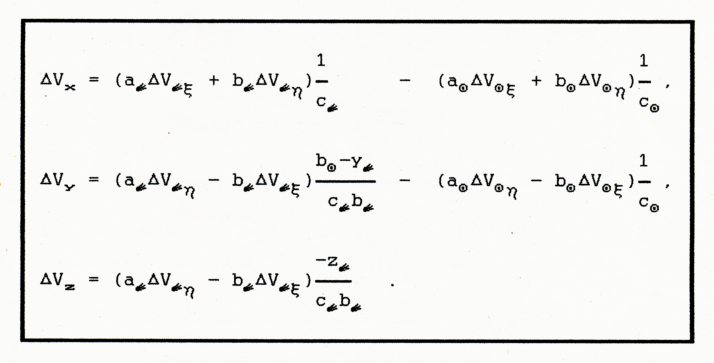
Ponieważ przedział <t1,t2> musi być wspólny dla wyliczania zmiany prędkości Słońca i komety, więc nawet jeśli wybierzemy go symetrycznie względem momentu największego zbliżenia gwiazdy do Słońca, to jest on ( poza szczególnymi przypadkami gdy x∈ = 0 ) niesymetryczny względem momentu największego zbliżenia gwiazdy do komety. Efekt wynikający z niesymetryczności, objawiający się głównie zmianą kierunku wektora przyrostu prędkości jest tym większy, im przedział <t1,t2> jest mniejszy. Z tego powodu, gdy porównuje się wyniki metody impulsowej z całkowaniem numerycznym, należy stosować powyższe wzory w pełnej postaci, gdyż całkowanie przeprowadza się zawsze na skończonym przedziale czasu.
Jeżeli natomiast stosujemy metodę impulsową do wyznaczania zmiany prędkości komety biorąc pod uwagę cały tor gwiazdy, czyli gdy <t1,t2> = <-∞,∞>, wówczas możemy podane wyżej wzory znacznie uprościć korzystając z formuł (D.14) otrzymanych w Dodatku. Wzory (2.4) przyjmą w tym przypadku postać:
(2.6)
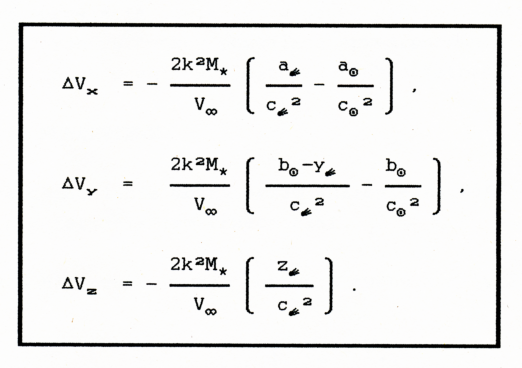
W tym samym układzie i stosując te same oznaczenia możemy dla porównania zapisać wzory klasycznej metody impulsowej następująco:
(2.7)
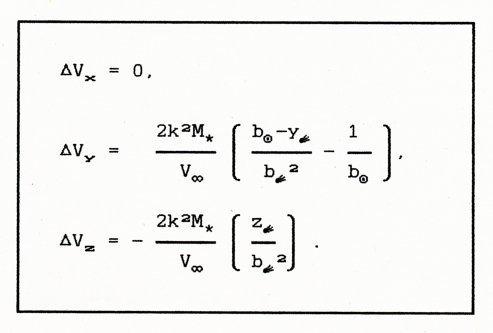
Jak widać metoda klasyczna pomija zmianę prędkości komety wzdłuż osi OX naszego układu, czyli wzdłuż prostoliniowego ( w wersji klasycznej ) toru gwiazdy, człon słoneczny w składowej ΔVy różni się o współczynnik co2/bo2 natomiast człony kometarne o współczynnik c∈2/b∈2 .
Zanim przystąpimy do dyskusji stosowalności metody impulsowej w różnych postaciach ( metoda klasyczna jest często dodatkowo modyfikowana przez całkowite pominięcie członu słonecznego lub kometarnego ), przedstawimy krótko sposób realizacji całkowania numerycznego w zagadnieniu zmiany orbity komety z obłoku Oorta pod wpływem przejścia gwiazdy w jego pobliżu. Jedynie wyniki takich dokładnych rachunków pozwalają przez porównanie z wynikami metod przybliżonych ocenić przydatność tych ostatnich.
CAŁKOWANIE NUMERYCZNE.
Rozważane zagadnienie można przez analogię nazwać ograniczonym, hiperbolicznym zagadnieniem trzech ciał.
W układzie heliocentrycznym równania ruchu komety mają postać:
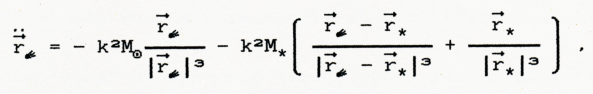
gdzie r∈ i r* oznaczają wektory wodzące odpowiednio komety i gwiazdy, k jest natomiast stałą grawitacji Gaussa. Do numerycznego całkowania tych ( skalarnie trzech ) równań zastosowane zostały dwie różne metody zalecane w literaturze: D2RKD7 ( Fox,1984; Dormand i Prince, 1978 ) oraz RA15 ( Everhart, 1985 ).
Są to metody jednokrokowe, rozwiązujące równania różniczkowe drugiego rzędu, z automatycznym doborem kroku. Listing procedury RA15 w Fortranie jest zamieszczony w cytowanej pracy, natomiast listing procedury D2RKD7, też w Fortranie, został udostępniony przez K.Foxa. Po przetłumaczeniu ich na język C i dokonaniu koniecznych adaptacji wykonane zostały rachunki testowe.
Potrzebne do wyliczania prawych stron równań pozycje gwiazdy otrzymywane były z formuł nieperturbowanego ruchu keplerowskiego. Obie metody dawały całkowicie zgodne wyniki choć RA15 w nieco krótszym czasie. Każde obliczenie prawej strony wymagało rozwiązania hiperbolicznego równania Keplera dla otrzymania pozycji gwiazdy. Stosowana była do tego celu bardzo szybka i dokładna metoda zaproponowana przez Odella i Goodinga (1988). Ponieważ uzyskanie wyników prezentowanych w dalszej części pracy wymagało całkowania bardzo dużej liczby przypadków, podjęta została próba skrócenia czasu obliczeń. Staranna organizacja procesu obliczeniowego, dobór odpowiednich jednostek, wreszcie odpowiednia wartość startowa kroku całkowania pozwoliły zmniejszyć czasochłonność o ok. 20%. Dopiero całkowita zmiana koncepcji, polegająca na rezygnacji z wyliczania pozycji gwiazdy ze wzorów analitycznych i dopisaniu równań ruchu gwiazdy do całkowanego numerycznie układu, pozwoliła na uzyskanie dalszego postępu. Efektem było dwukrotne przyspieszenie rachunków procedurą D2RKD7, przy nie zmienionym czasie realizacji dla RA15.
Należy podkreślić, że ten zaskakujący być może rezultat jest wynikiem niezwykle prostej postaci prawych stron równań ruchu gwiazdy. Duże znaczenie miał też wybór układu odniesienia, dzięki któremu należało dodatkowo całkować tylko dwa równania, gdyż ruch gwiazdy odbywa się zawsze w płaszczyźnie OXY przyjętego układu.
Z przyczyn podanych wyżej do zasadniczych rachunków w tej pracy użyto metody D2RKD7. Badania dokładności rozwiązania pokazały, że metoda ta daje bardzo dobre wyniki nawet przy bardzo bliskich przejściach gwiazdy obok Słońca lub komety.

