Autorem poniższego opracowania (wraz z rysunkami) jest dr Piotr A. Dybczyński z Instytutu Obserwatorium Astronomiczne UAM w Poznaniu.
O równaniu Keplera

Johannes Kepler
(Wikimedia Commons)
W przypadku eliptycznym równanie Keplera ma postać:
M = E - e sin(E)
gdzie M jest anomalią średnią (w radianach), E jest anomalią mimośrodową (też w radianach) a e jest mimośrodem. Przypadek gdy e = 0 nie jest interesujący, będziemy więc dalej zakładać, że 0 < e < 1 .
Równanie to ma zasadnicze znaczenie gdy wyliczamy pozycje ciała na eliptycznej orbicie keplerowskiej, dlatego opracowano wiele różnych, często bardzo zaawansowanych, metod numerycznych jego rozwiązywania, nastawionych na dużą dokładność i szybkość rachunków. Ważnym elementem większości z nich jest wybór punktu startowego danej metody.
Jak ktoś nie liznął jeszcze mechaniki nieba niech traktuje to równanie jako przykład trygonometrycznego równania przestępnego do rozwiązania numerycznego.
Spróbujmy na początek rozwiązać to równanie graficznie
Pomoże to zarówno zrozumieć naturę zagadnienia jak i wybrać odpowiednią daną lub dane startowe do metod opisanych niżej.
Przepiszmy równanie Keplera tak:
E = M + e sin(E)
i zinterpretujmy je jako poszukiwanie punktu przecięcia się wykresów dwóch funkcji anomalii mimośrodowej:
f1(E) = E,
f2(E) = M + e sin(E).
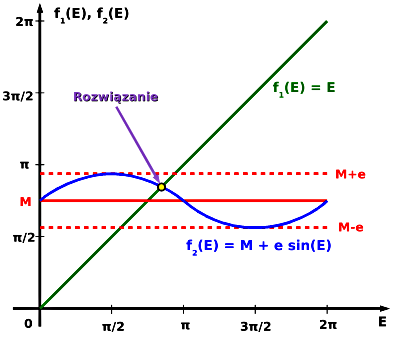
Rysunek 1.
Zagadnienie to przedstawia Rysunek 1.
Ze względów oczywistych ograniczamy się do kwadratu 2π × 2π .
Na osi poziomej mamy anomalię mimośrodową E a na osi pionowej wykresy obu funkcji f1(E) = E oraz f2(E) = M + e sin(E) .
Widać wyraźnie, że nasze równanie ma rozwiązanie zawsze, i tylko jedno. Widać też np., że rozwiązanie to jest zawsze w przedziale <M-e ; M+e>.
Pięć prostych metod numerycznego rozwiązywania eliptycznego równania Keplera
1. Metoda iteracji prostej
Korzysta ona z równania Keplera w postaci: E = M + e sin(E), na bazie którego tworzymy formułę dla wyliczania kolejnych przybliżeń:
En+1 = M + e sin(En )
Metoda ta jest dla tego równania zawsze zbieżna. Wybór wartości startowej Eo pozostawiam Państwa inwencji.
Rachunki przerywamy gdy | En+1 - En | < ε, gdzie ε jest małą liczbą, dla testów może to być 10-7 ale docelowo 10-12. Nie oznacza to, że rozwiązanie znamy z dokładnością ε, ale w praktyce dokładność jest nie wiele gorsza.
2. Metoda Newtona (stycznych)
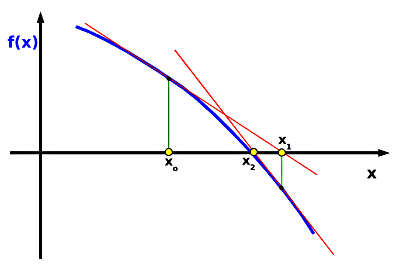
Rysunek 2.
Geometryczna interpretacja metody Newtona
Ta i wszystkie następne metody korzystają z równania Keplera przepisanego jako:
f(E) = M + e sin(E ) - E = 0
szukamy zatem miejsca zerowego funkcji f(E). Jest to bardzo popularne zagadnienie, w naszym przypadku tym łatwiejsze, że wiemy iż takie miejsce istnieje i jest tylko jedno.
Wzór dla metody Newtona ma postać
En+1 = En - f(En) / f ' (En)
gdzie f ' (En) oznacza pochodną funkcji f(E) po E , wyliczoną w punkcie En . Wyprowadzenie wzoru na tę pochodną nie jest trudne ![]() .
.
Metoda wymaga wybrania dogodnej wartości startowej Eo , której wybór pozostawiam Państwu. Dla źle wybranej danej startowej metoda może nie być zbieżna.
Podobnie jak poprzednio rachunki przerywamy gdy | En+1 - En | < ε, gdzie ε jest małą liczbą, dla testów może to być 10-7 ale docelowo 10-12. Tu również nie oznacza to, że rozwiązanie znamy z dokładnością ε, ale w praktyce dokładność jest porównywalna.
3. Metoda bisekcji (czyli połowienia)
Metoda ta jest jedną z wolniejszych ale daje rozwiązanie zawsze i to ze z góry zadaną dokładnością. Jako punkt wyjścia musimy podać tzw. "przedział izolacji rozwiązania", czyli dwie wartości anomalii mimośrodowej E, nazwijmy je a i b, takie że dokładnie jedno rozwiązanie jest w przedziale <a, b>. Zakładając, że rozwiązaniem nie jest ani a ani b oznacza to, że funkcja f(E) = M + e sin(E ) - E ma w tych punktach różne znaki (bo rozwiązanie, czyli miejsce zerowe funkcji f(E) ma leżeć pomiędzy nimi).
Oczywiście z braku lepszego pomysłu można wziąć a = 0 oraz b = 2π.
Wzór na wyliczenie kolejnego przybliżenia ma trywialną postać:
c = (a + b) / 2
czyli bierzemy środek przedziału <a, b>. Teraz do następnej iteracji bierzemy tę połowę przedziału <a, b>, na końcach której funkcja f(E) ma różne znaki, czyli badamy warunek:
f(a) · f(c) < 0
Jeśli warunek jest prawdziwy nowym przedziałem do połowienia jest właśnie <a, c>, jeśli jest fałszywy to do dalszych rachunków bierzemy przedział <c, b>. jak znajdę czas to napiszę tłumaczenie opisu tej funkcji, póki co szukaj Aby osiągnąć dokładność ε należy wykonać n połowień, przy czym n wyliczamy ze wzoru :
ε = |b - a| / 2n
mając zadaną dokładność ε (trzeba sobie przypomnieć o logarytmach ![]() ).
).
4. Metoda siecznych
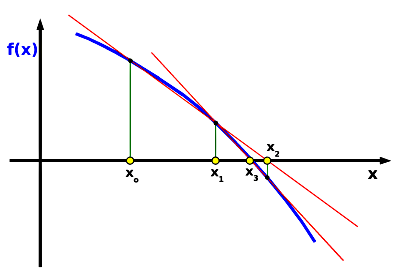
Rysunek 3.
Geometryczna interpretacja metody siecznych
Jest to wariant metody Newtona, w którym pochodną zastąpiono ilorazem różnicowym. Wzór na kolejne przybliżenia ma postać:
En+1 = En - ( f(En)(En - En-1) ) / (f(En) - f(En-1) )
Dodatkowe nawiasy w powyższym wzorze nie są przypadkiem, kolejność rachunków jest tu bardzo ważna.
Widać, że metoda do startu potrzebuje dwóch wartości początkowych E0 i E1, z których wyliczamy E3 itd. Wybór danych startowych pozostawiam Państwa inwencji, nie muszą one leżeć po obu stronach rozwiązania. Uwaga: źle wybrane dane startowe nie gwarantują zbieżności metody.
Podobnie jak poprzednio rachunki przerywamy gdy | En+1 - En | < ε, gdzie ε jest małą liczbą, dla testów może to być 10-7 ale docelowo 10-12. Tu również nie oznacza to, że rozwiązanie znamy z dokładnością ε, ale w praktyce dokładność jest porównywalna.
5. Metoda "regula falsi"
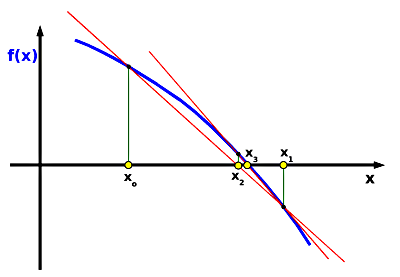
Rysunek 4.
Geometryczna interpretacja metody "regula falsi"
Jest to kombinacja dwóch poprzednich metod, połowienia i siecznych. Do startu potrzebny jest "przedział izolacji rozwiązania", czyli dwie wartości anomalii mimośrodowej E, nazwijmy je a i b, takie że dokładnie jedno rozwiązanie jest w przedziale <a, b> jak w metodzie bisekcji. Tu jednak punkt c podziału tego przedziału wyliczamy z równania pochodzącego z metody siecznych:
c = b - ( f(b)(b - a) ) / (f(b) - f(a) )
gdzie oczywiście funkcja f() to f(E) = M + e sin(E ) - E.
Do następnej iteracji bierzemy tę część przedziału <a, b>, na końcach której funkcja f(E) ma różne znaki, czyli badamy znany z metody bisekcji warunek:
f(a) · f(c) < 0
Jeśli warunek jest prawdziwy, nowym przedziałem do połowienia jest <a, c>, jeśli jest fałszywy, to do dalszych rachunków bierzemy przedział <c, b>.
Różnica jest taka, że metoda ta jest zwykle znacznie szybciej zbieżna niż metoda bisekcji, nie da się jednak z góry wyliczyć ile podziałów trzeba wykonać a jedyną kontrolą dokładności jest długość ostatnio otrzymanego przedziału. Rozwiązanie otrzymujemy jednak zawsze, w odróżnieniu od metody "siecznych".


