Autorem poniższego opracowania (wraz z rysunkami, chyba że podane jest inne żródło) jest dr Piotr A. Dybczyński z Instytutu Obserwatorium Astronomiczne UAM w Poznaniu.
Zadanie 4 - Praca z katalogiem Tycho-2 (wersja 3, rok akad. 2014/2015)
W zadaniu tym będziemy wybierać podzbiór katalogu Tycho-2, zawierający wszystkie gwiazdy odległe o mniej niż 4 stopnie od podanego przez użytkownika punktu o współrzędnych (α, δ).
Katalog TYCHO-2 znajduje się na dysku w pracowni studenckiej w folderze:
/home/COMMON/katalogi/tycho2
Do wykonania zadania potrzebne nam będą pliki:
..../tycho2/docs/guide.pdf
..../tycho2/data/catalog.dat
..../tycho2/data/index.dat
Pierwszy plik to dokumentacja elektronicznej wersji katalogu (jest też tam dostępna w wersji postscriptowej), niezbędna do korzystania z danych. Z tego dokumentu zaczerpnąłem Tabele 1,2 i 4.
Drugi plik, to główny plik z danymi (pliki z suplementami nas w tym zadaniu nie interesują).
Plik trzeci to tzw. plik indeksu, więcej o nim niżej.
Jeśli ktoś będzie chciał pracować poza pracownią musi sobie odpowiednie pliki skopiować lub pobrać z internetu:
ftp://cdsarc.u-strasbg.fr/pub/cats/I/259
Strukturę plików z danymi przedstawia tabela 1:
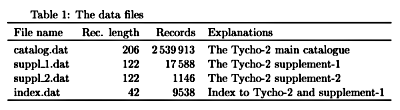
W pierwszej kolumnie mamy nazwę pliku (interesują nas tylko pierwszy i ostatni), w drugiej mamy długość wiersza w bajtach (znakach). Z punktu widzenia języka C długości te trzeba zwiększyć o 2, gdyż na końcu każdej linii są dwa "kody końca wiersza" \CR\LF.
W trzeciej kolumnie mamy informacje o liczbie wierszy w pliku. Główny katalog zawiera więc informacje o 2539913 gwiazdach a plik indeksowy opisuje 9538 pól.
Jak łatwo się więc domyślić, pliki te to zwykłe pliki tekstowe (można je np. w Midnight Commanderze oglądać klawiszem F3).
Poniżej mamy początki pierwszych 13 wierszy katalogu Tycho-2 (z pliku catalog.dat):
0001 00008 1| | 2.31750494| 2.23184345| -16.3| -9.0| 68| 73| 1.7| 1.8|1958... 0001 00013 1| | 1.12558209| 2.26739400| 27.7| -0.5| 9| 12| 1.2| 1.2|1990... 0001 00016 1| | 1.05686490| 1.89782870| -25.9| -44.4| 85| 99| 2.1| 2.4|1959... 0001 00017 1|P| 0.05059802| 1.77144349| 32.1| -20.7| 21| 31| 1.6| 1.6|1989... 0001 00017 2|P| 0.05059802| 1.77144349| 32.1| -20.7| 21| 31| 1.6| 1.6|1989... 0001 00020 1| | 0.37220148| 2.48018803| 9.3| -58.8| 55| 75| 1.8| 1.9|1977... 0001 00022 1| | 1.02766471| 1.45849152| 37.5| -10.6| 56| 47| 1.8| 1.8|1970... 0001 00024 1| | 0.77431739| 1.71059531| 34.3| 22.3| 73| 88| 2.0| 2.2|1968... 0001 00036 1| | 0.29838646| 1.92361761| 200.1| -211.7| 46| 60| 1.4| 1.5|1976... 0001 00039 1| | 2.37141849| 2.30400355| 13.5| -13.5| 12| 13| 1.3| 1.2|1990... 0001 00041 1|X| | | | | | | | | ... 0001 00049 1| | 1.08234017| 2.12262034| 22.6| -4.5|108|132| 2.8| 3.2|1965... 0001 00054 1| | 0.87806836| 2.31596792| -21.1| -18.3| 46| 43| 1.8| 1.9|1976...
Jak widać pola są oddzielone pionową kreską, niektóre pola składają się z kilku liczb a niektóre są puste!
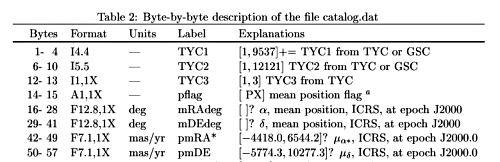
Dokładny format każdego wiersza opisuje Tabela 2, której początek widzimy obok. Pierwsza kolumna mówi które bajty zajmują dane.
Przypominam, że w języku C będziemy je numerować od zera a nie od jedynki!
Druga kolumna to format danych opisany w konwencji Fortranowskiej. I5.5 oznacza tu liczbę całkowitą i pięciocyfrową, A1 oznacza ciąg liter składający się tu z 1 litery, 1X oznacza bajt do pominięcia (odpowiada pionowej kresce w pliku) a F12.8 oznacza daną zmiennoprzecinkową, zajmującą w sumie z kropką i ewentualnym znakiem 12 bajtów, w tym osiem cyfr po kropce dziesiętnej.
Pierwsze pole składa się z trzech liczb całkowitych:
- TYC1 - czterocyfrowego numeru pola GSC, z ciągłego zakresu od 1 do 9537, ściśle niemalejąco
- TYC2 - pięciocyfrowego numeru kolejnego gwiazdy w danym polu. W ramach tego samego pola numery są niemalejące ale niekoniecznie ciągłe.
- TYC3 - jednocyfrowej liczby z zakresu 1-3, oznaczającej kolejny składnik układu wielokrotnego.
Drugie pole (bajt czternasty) to albo spacja albo jedna z liter P lub X. Spacja oznacza normalną gwiazdę, P pojawia się w sytuacji, gdy dla więcej niż jednej gwiazdy podane są współrzędne fotocentrum z braku możliwości rozdzielenia składników. Wszystkie wiersze z literą P bierzemy pod uwagę, natomiast litera X oznacza brak danych (α,δ) i wiersze takie pomijamy!
Jak czytamy dane z plików?
Otóż będziemy używali zestawu dwóch funkcji biblioteki stdio: fgets() i sscanf().
Funkcja fgets
Funkcja sscanf()
jest kolejną z rodziny scanf() i fscanf, tylko zamiast ze standardowego wejścia lub z pliku czyta z bufora w pamięci, np. z tablicy znakowej.
Dla przykładu taki kawałek kodu:
int main(void)
{
char buff[212],znak;
FILE * f;
int tyc1, tyc2, tyc3;
double alfa, delta;
f=fopen("/home/COMMON/katalogi/tycho2/data/catalog.dat","r");
if(f==NULL) return 1;
fgets(buff,210,f);
sscanf(buff+13,"%c",&znak);
if(znak != 'X')
{
sscanf(buff," %d %d %d",&tyc1, &tyc2, &tyc3);
sscanf(buff+15," %lf",&alfa);
sscanf(buff+28," %lf",&delta);
}
/* .... */
czyta pierwszy wiersz katalogu Tycho-2 i z niego wszystkie potrzebne nam dane, jeśli istnieją.
Jak wykorzystać plik index.dat ?
Nie będziemy czytać wszystkich 2.5 miliona wierszy katalogu Tycho-2 tylko wybrane pola GSC.
N-ty wiersz pliku index.dat w pierwszej kolumnie zawiera numer wiersza z pliku catalog.dat, w którym zaczynają się gwiazdy N-tego pola.
Jeśli odczytamy ten numer wiersza to wykorzystując kolejną, nową funkcję języka C fseek(), ustawimy "kursor" czytania pliku catalog.dat właśnie na ten wiersz.
Funkcja: fseek
W zasięgu deklaracji z poprzedniego przykładu kodu, instrukcje:
/* ... */
fseek(f,208*1111,SEEK_SET);
fgets(buff,210,f);
sscanf(buff+13,"%c",&znak);
if(znak != 'X')
{
sscanf(buff," %d %d %d",&tyc1, &tyc2, &tyc3);
sscanf(buff+15," %lf",&alfa);
sscanf(buff+28," %lf",&delta);
}
/* .... */
przeczytają dane nie z pierwszego wiersza katalogu tylko dane z wiersza 1111-tego. Numer 1111 jest tu zupełnie przypadkowy, np. aby przeczytać dane o pierwszej gwieździe z szóstego pola GSC należy czytać wiersz 873.
A skąd wiadomo, które pola GSC nas interesują ?
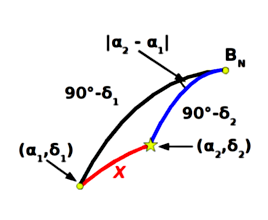
Rysunek 3.
Wracamy tu do definicji naszego zadania. Na Rysunku 3 mamy pokazany trójkąt sferyczny, którego jednym wierzchołkiem jest biegun, drugim środek naszego pola (α1, δ1 ) a trzecim gwiazda o współrzędnych (α2, δ2 ). Jeśli chcemy ustalić w jakiej odległości od środka pola znajduje się gwiazda (wybieramy te o odległości mniejszej niż 4 °) to trzeba wyliczyć długość boku x tego trójkąta.
Trygonometria sferyczna mówi, że gdy znamy boki a i b oraz kąt C między nimi to:
- bok c wyliczamy ze wzoru cosinusów: cos c = cos a cos b + sin a sin b cos C .
W naszym przypadku bok a = 90° - δ1 , bok b = 90° - δ2 a kąt C = |α1 - α2|. Rozwiązanie jednoznaczne uzyskujemy dzięki wiedzy, że kąt C i bok c (na rysunku x ) są rzędu kilku stopni.
Skoro umiemy już rozstrzygnąć, czy punkt o współrzędnych (α,δ) należy do naszego koła o promieniu 4° to skorzystajmy w pełni z pliku indeksowego.

Format tego pliku opisany jest w Tabeli 4. Powtórzmy: n-ty wiersz pliku index.dat w pierwszej kolumnie zawiera numer wiersza z pliku catalog.dat, w którym zaczynają się gwiazdy n-tego pola GSC (TYC1).
A skąd mamy wiedzieć, czy dane pole GSC nas interesuje? O tym decydują dalsze informacje z tego samego wiersza: kolumnę drugą pomijamy a kolumny od 3 do 6 zawierają odpowiednio najmniejszą i największą rektascensję i deklinację gwiazd występujących w danym polu, zgodnie z opisem w Tabeli 4.
Wszystkie cztery liczby zapisane są w stopniach z dwiema cyframi po przecinku (deklinację może poprzedzać minus).
Poniżej mamy pokazane kilka pierwszych i kilka ostatnich wierszy z pliku index.dat:
1| 1| 0.00| 2.49| 0.00| 2.49
168| 1| 2.50| 5.00| 0.00| 2.50
341| 5| 5.00| 7.49| 0.04| 2.50
497| 5| 0.00| 2.49| 2.50| 5.00
705| 7| 2.51| 5.00| 2.52| 4.99
873| 9| 5.00| 7.50| 2.52| 4.98
1026| 9| 0.01| 2.50| 5.00| 7.48
.
.
.
2539704| 17589|241.48|269.63|-89.87|-88.17
2539757| 17589|270.62|298.55|-89.67|-88.17
2539806| 17589|300.13|329.48|-89.71|-88.13
2539865| 17589|330.85|359.50|-89.70|-88.14
2539914| 17589| 0.00| 0.00| 0.00| 0.00
Z trzeciego wiersza wynika np., że trzecie pole GSC zaczyna się w 341 wierszu pliku catalog.dat, a zawarte w tym polu gwiazdy mają rektascensje z przedziału od 5 do 7.49 stopnia a deklinacje od 0.04 do 2.5 stopnia. Wiedząc gdzie użytkownik naszego programu umieścił środek pola oraz znając jego promień (4°) potrafimy na podstawie tych danych jednoznacznie rozstrzygnąć, czy to pole GSC dotyka choćby naszego pola, czy też jest całkowicie do pominięcia, bo żadna znajdująca się w nim gwiazda nie może znaleźć się w polu.
Jak dotąd struktura naszego programu wygląda następująco:
- Pytamy użytkownika o środek pola.
- Kopiujemy do odpowiednio zadeklarowanej tablicy te wiersze katalogu Tycho-2, które opisują gwiazdy z pola. W tym celu:
- Otwieramy pliki index.dat oraz catalog.dat .
- Czytamy kolejno wiersze pliku index.dat i decydujemy, czy opisywane pole GSC zahacza o nasze pole.
- Jeśli tak, skaczemy do odpowiedniego wiersza pliku catalog.dat (funkcją fseek() opisaną wyżej) i czytamy kolejno wiersze opisujące każdą gwiazdę pola GSC, kopiując do tablicy tylko te, które opisują gwiazdy z pola o podanym przez użytkownika środku i promieniu 4°.
- Jeśli nie to pomijamy o pole GSC i czytamy następny wiersz pliku index.dat .
- Gdy dojdziemy do końca pliku index.dat (ma on specjalną zawartość co widać wyżej) mamy przejrzany cały katalog Tycho-2 i skopiowane dane opisujące wszystkie gwiazdy tego katalogu leżące w wybranym polu. Nie zapomnijmy w tym miejscu zamknąć plików index.dat oraz catalog.dat .
'''Kilka słów komentarza: jak zadeklarować tablicę na kopiowane wiersze katalogu i jak te wiersze umieszczać w tablicy.
Kilka słów komentarza: jak zadeklarować tablicę na kopiowane wiersze katalogu i jak te wiersze umieszczać w tablicy.
Oto podpowiedź:
/* użycie niżej funkcji kopiowania łańcuchów znaków strcpy()
wymaga nowego pliku nagłówkowego: */
#include<string.h>
/* na początku kodu definiujemy maksymalną liczbę obsługiwanych gwiazd.
W czasie testowania programu może to być np. 1000 albo 10000
do zaliczenia przystępujemy z definicją: */
#define MAX (100000)
/* korzystając z tej definicji deklarujemy w programie tablicę: */
char A[MAX][210];
/* tablica ta pomieści MAX wierszy po 210 znaków (lekki zapas nie zaszkodzi) */
k=0; /* k- liczbę skopiowanych gwiazd - zerujemy tylko przed czytaniem pierwszego pola ! */
/* jeśli teraz w zmiennej pole mamy numer pola GSC to z pliku index.dat, z wiersza o numerze pole
możemy z pierwszej kolumny odczytać w jakim wierszu pliku catalog.dat zaczynają się gwiazdy tego pola.
Jeśli ten numer wiersza przechowamy w zmiennej wiersz, to: */
fseek(f,208*wiersz,SEEK_SET); /* skacze do odpowiedniego wiersza katalogu */
while(fgets(buff,300,f) != NULL) /* dopóki są dane */
{
sscanf(buff," %d",&tyc1);
if(tyc1 != pole) break; /* koniec gwiazd tego pola */
sscanf(buff+13,"%c",&znak);
if(znak != 'X')
{
strcpy(&A[k][0],buff);
k = k+1; //skopiowaliśmy kolejną gwiazdę
/* lub skrótowo: strcpy(A[k++],buff); */
}
else continue; /* wiersz bez danych */
if(k==MAX) break; /* zapełniona tablica */
}
/* .... */
Na pracowni w katalogu /home/COMMON/dydaktyka/PAD_programowanie/ jest mój program o nazwie tycho_test_2, który realizuje opisane wyżej czynności, podając na końcu ile gwiazd z katalogu Tycho-2 pobrał. Mój program dodatkowo sortuje wybrane gwiazdy według rektascensji i deklinacji i wypisuje pierwsze i ostatnie dziesięć sztuk po każdym sortowaniu. To Państwa czeka w następnym etapie.
Proszę potraktować powyższy opis jako pierwszą część zadania i zacząć pisać program wybierający poprawnie tyle samo gwiazd.
Na tym etapie proszę koniecznie przeczytać i usilnie spróbować zrozumieć Rozdział 5 "Wskaźniki i tablice" z podręcznika Kernighana & Ritchie-go!
Można pominąć podrozdziały: 5.10, 5.11 i 5.12. ![]()
Po przestudiowaniu podręcznika proszę sprawdzić swoją wiedzę czytając ten materiał
Co dalej?
Teraz mając wybrane i skopiowane do tablicy wiersze interesujących nas gwiazd należy je posortować według rektascensji.
Stosować będziemy najprostszy chyba algorytm sortowania, tzw. sortowanie bąbelkowe. Ładny materiał na ten temat można znaleźć pod adresem: http://www.home.umk.pl/~abak/wdimat/s/BubbleSort.html .
Warto pobawić się zawartym tam apletem by oswoić się z działaniem tego algorytmu.
A po co uczyliśmy się o wskaźnikach (pointerach)?
Otóż sortowania nie będziemy realizować przestawiając zgodnie z algorytmem "bąbelkowym" całych wierszy tablicy zawierającej kopie fragmentu katalogu. Zamiast tego stworzymy tablicę wskaźników do wierszy tej pierwszej tablicy i sortować będziemy przestawiając jedynie wskaźniki!
Poniższy kod pokazuje jak zadeklarować tablice A i B oraz jak tę ostatnią zainicjować:
#define MAX (100000)
char A[MAX][210];
char * B[MAX];
/* ... tu wybieramy gwiazdy i wstawiamy wiersze do tablicy A[][]... */
for(i=0;i<MAX;++i) B[i] = &A[i][0];
/* lub krócej ale mniej czytelnie:
for(i=0;i<MAX;++i) B[i] = A[i]; */
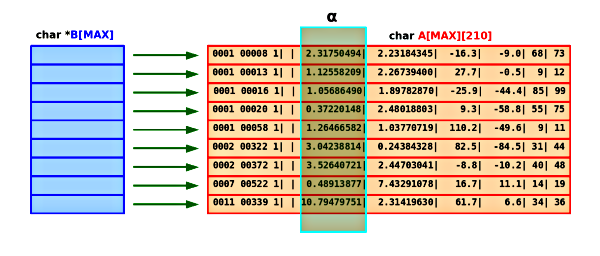
Rys.4. Tablice przed sortowaniem.
W ten sposób pierwszy element tablicy B[] wskazuje PRZED SORTOWANIEM na pierwszy znak pierwszego wiersza tablicy A[][], drugi na pierwszy znak drugiego itd., jak to pokazano na Rysunku 4.
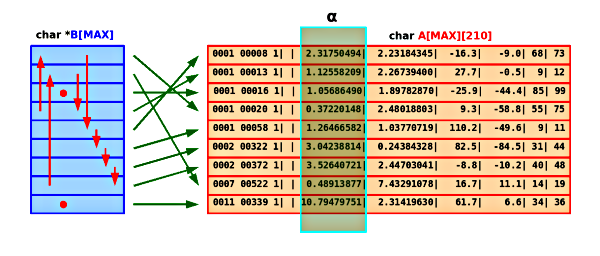
Rys.5. Tablice po sortowaniu.
Jeśli założyć, że sortujemy rosnąco według rektascencji (wyróżniona kolumna na rysunkach 4 i 5) to po sortowaniu elementy tablicy B[] powinny wskazywać początki wierszy tablicy A[][] jak na Rysunku 5.
Zamiast "miotać" ponad dwustu-bajtowymi wierszami tablicy A[][] przemieszczamy jedynie kilku-bajtowe elementy tablicy B[] (czerwone strzałki na Rys.5.).
Ale jak sortować elementy tablicy B[]?
Przecież porównywanie zawartych w nich wskaźników (pointerów, adresów) nie ma sensu!!
Mamy posortować gwiazdy wybranego pola, malejąco według rektascensji. Czyli o ewentualnej zamianie elementów tablicy B[] musi decydować odpowiednia rektascensja gwiazdy, której wiersz jest wskazywany przez dany element tablicy B[] !
Podpowiedź jak to zrobić jest w poniższym kawałku kodu. Korzystamy tu z poznanej wyżej funkcji sscanf() . Jeśli, jak na rysunkach 4 i 5, sortujemy malejąco według rektascencji, to decyzja, czy zamienić elementy B[i] oraz B[i+1] wymaga czegoś w rodzaju:
char * zapas;
/* magiczna liczba 15 poniżej wynika z faktu, że czytamy rektascensję.
Dla deklinacji byłoby to 28 */
sscanf(B[i]+ 15," %lf",&alfa1);
sscanf(B[i+1]+ 15," %lf",&alfa2);
if(alfa1>alfa2) {
zapas = B[i];
B[i] = B[i+1];
B[i+1] = zapas;
}
Zwracam uwagę, że tylko przy porównywaniu elementów B[0] oraz B[1] musimy dwa razy wywołać (bardzo czasochłonną!) funkcję sscanf(). Przy każdym następnym porównaniu pierwszą rektascencję mamy już przeczytaną proszę więc tak zorganizować program by z tego faktu skorzystać. Obowiązkowo.
Skoro umiemy "porównać" dwa kolejne elementy tablicy B[] i wcześniej poznaliśmy (i przećwiczyli) algorytm sortowania bąbelkowego, to na tym etapie nasz program ma już gwiazdy posortowane. Czytanie skopiowanych z katalogu wierszy według kolejności zapisanej w tablicy B[] dostarczy nam właśnie posortowanych danych o gwiazdach.
Teraz już tylko wypiszemy pierwsze dziesięć i ostatnie 10 numerów (TYC1,TYC2 i TYC3) gwiazd z naszego podzbioru i koniec zadania.



