Autorem poniższego opracowania (wraz z rysunkami, chyba że podane jest inne żródło) jest dr Piotr A. Dybczyński z Instytutu Obserwatorium Astronomiczne UAM w Poznaniu.
Zadanie 4 - Praca z katalogiem Tycho-2 w wersji dla specjalności informatycznej
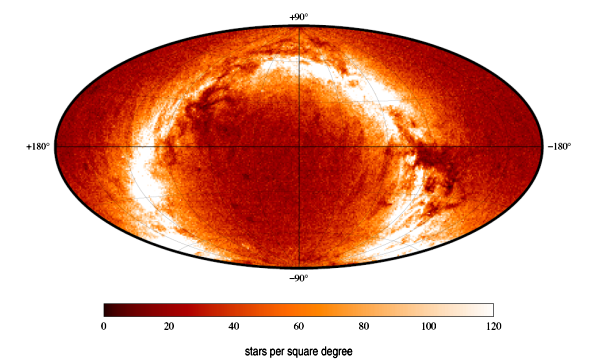
Rys.1 b Gęstość gwiazd katalogu Tycho-2 na sferze niebieskiej we
współrzędnych równikowych. W najgęstszych rejonach przekracza ona 320
gwiazd/stopień kwadratowy. Średnio waha się od 25 gwiazd/stopień kwadratowy
w rejonie biegunów Galaktycznych do 150 w pasie Drogi Mlecznej
(z "Guide to the Tycho-2 catalogue").
W zadaniu tym będziemy wybierać podzbiór katalogu Tycho-2 a następnie wyznaczać i przedstawiać w formie histogramu gęstość polową gwiazd w wybranym podzbiorze.
Katalog TYCHO-2 znajduje się na dysku w pracowni studenckiej w folderze:
/home/COMMON/katalogi/tycho2
Do wykonania zadania potrzebne nam będą pliki:
..../tycho2/docs/guide.pdf
..../tycho2/data/catalog.dat
..../tycho2/data/index.dat
Jeśli ktoś będzie chciał pracować poza pracownią musi sobie odpowiednie pliki skopiować lub pobrać z internetu:
ftp://cdsarc.u-strasbg.fr/pub/cats/I/259
Pierwszy plik to dokumentacja elektronicznej wersji katalogu (jest też tam dostępna w wersji postscriptowej), niezbędna do korzystania z danych. Z tego dokumentu zaczerpnąłem zarówno Rysunek 1 jak i Tabele 1,2 i 4.
Drugi plik, to główny plik z danymi (pliki z suplementami nas w tym zadaniu nie interesują).
Plik trzeci to tzw. plik indeksu, więcej o nim niżej.
Strukturę tych plików przedstawia tabela 1:
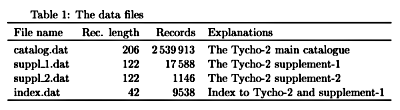
W pierwszej kolumnie mamy nazwę pliku (interesują nas tylko pierwszy i ostatni), w drugiej mamy długość wiersza w bajtach (znakach). Z punktu widzenia języka C długości te trzeba zwiększyć o 2, gdyż na końcu każdej linii są dwa "kody końca wiersza" \CR\LF.
W trzeciej kolumnie mamy informacje o liczbie wierszy w pliku. Główny katalog zawiera więc informacje o 2539913 gwiazdach a plik indeksowy opisuje 9538 pól.
Jak łatwo się więc domyślić, pliki te to zwykłe pliki tekstowe (można je np. w Midnight Commanderze oglądać klawiszem F3).
Poniżej mamy początki pierwszych 13 wierszy katalogu Tycho-2 (z pliku catalog.dat):
0001 00008 1| | 2.31750494| 2.23184345| -16.3| -9.0| 68| 73| 1.7| 1.8|1958... 0001 00013 1| | 1.12558209| 2.26739400| 27.7| -0.5| 9| 12| 1.2| 1.2|1990... 0001 00016 1| | 1.05686490| 1.89782870| -25.9| -44.4| 85| 99| 2.1| 2.4|1959... 0001 00017 1|P| 0.05059802| 1.77144349| 32.1| -20.7| 21| 31| 1.6| 1.6|1989... 0001 00017 2|P| 0.05059802| 1.77144349| 32.1| -20.7| 21| 31| 1.6| 1.6|1989... 0001 00020 1| | 0.37220148| 2.48018803| 9.3| -58.8| 55| 75| 1.8| 1.9|1977... 0001 00022 1| | 1.02766471| 1.45849152| 37.5| -10.6| 56| 47| 1.8| 1.8|1970... 0001 00024 1| | 0.77431739| 1.71059531| 34.3| 22.3| 73| 88| 2.0| 2.2|1968... 0001 00036 1| | 0.29838646| 1.92361761| 200.1| -211.7| 46| 60| 1.4| 1.5|1976... 0001 00039 1| | 2.37141849| 2.30400355| 13.5| -13.5| 12| 13| 1.3| 1.2|1990... 0001 00041 1|X| | | | | | | | | ... 0001 00049 1| | 1.08234017| 2.12262034| 22.6| -4.5|108|132| 2.8| 3.2|1965... 0001 00054 1| | 0.87806836| 2.31596792| -21.1| -18.3| 46| 43| 1.8| 1.9|1976...
Jak widać pola są oddzielone pionową kreską, niektóre pola składają się z kilku liczb a niektóre są puste!
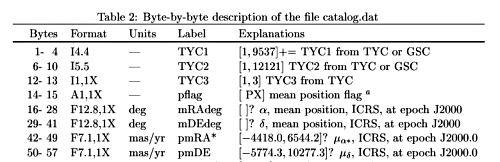
Dokładny format każdego wiersza opisuje Tabela 2, której początek widzimy obok. Pierwsza kolumna mówi które bajty zajmują dane.
Przypominam, że w języku C będziemy je numerować od zera a nie od jedynki!
Druga kolumna to format danych opisany w konwencji Fortranowskiej. I5.5 oznacza tu liczbę całkowitą i pięciocyfrową, A1 oznacza ciąg liter składający się tu z 1 litery, 1X oznacza bajt do pominięcia (odpowiada pionowej kresce w pliku) a F12.8 oznacza daną zmiennoprzecinkową, zajmującą w sumie z kropką i ewentualnym znakiem 12 bajtów, w tym osiem cyfr po kropce dziesiętnej.
Pierwsze pole składa się z trzech liczb całkowitych:
- TYC1 - czterocyfrowego numeru pola GSC, z ciągłego zakresu od 1 do 9537, ściśle niemalejąco
- TYC2 - pięciocyfrowego numeru kolejnego gwiazdy w danym polu. W ramach tego samego pola numery są niemalejące ale niekoniecznie ciągłe.
- TYC3 - jednocyfrowej liczby z zakresu 1-3, oznaczającej kolejny składnik układu wielokrotnego.
Drugie pole (bajt czternasty) to albo spacja albo jedna z liter P lub X. Spacja oznacza normalną gwiazdę, P pojawia się w sytuacji, gdy dla więcej niż jednej gwiazdy podane są współrzędne fotocentrum z braku możliwości rozdzielenia składników. Wszystkie wiersze z literą P bierzemy pod uwagę, natomiast litera X oznacza brak danych (α,δ) i wiersze takie pomijamy!
Jak czytamy dane z plików?
Otóż będziemy używali zestawu dwóch funkcji biblioteki stdio: fgets() i sscanf().
NAZWA fgets
Funkcja sscanf()
jest kolejną z rodziny scanf() i fscanf, tylko zamiast ze standardowego wejścia lub z pliku czyta z bufora w pamięci, np. z tablicy znakowej.
Dla przykładu taki kawałek kodu:
int main(void)
{
char buff[212],znak;
FILE * f;
int tyc1, tyc2, tyc3;
double alfa, delta;
f=fopen("/home/COMMON/katalogi/tycho2/data/catalog.dat","r");
if(f==NULL) return 1;
fgets(buff,210,f);
sscanf(buff+13,"%c",&znak);
if(znak != 'X')
{
sscanf(buff," %d %d %d",&tyc1, &tyc2, &tyc3);
sscanf(buff+15," %lf",&alfa);
sscanf(buff+28," %lf",&delta);
}
/* .... */
czyta pierwszy wiersz katalogu Tycho-2 i z niego wszystkie potrzebne nam dane, jeśli istnieją.
Jak wykorzystać plik index.dat ?
Nie będziemy czytać wszystkich 2.5 miliona wierszy katalogu Tycho-2 tylko wybrane pola GSC.
N-ty wiersz pliku index.dat w pierwszej kolumnie zawiera numer wiersza z pliku catalog.dat, w którym zaczynają się gwiazdy N-tego pola.
Jeśli odczytamy ten numer wiersza to wykorzystując kolejną, nową funkcję języka C fseek(), ustawimy "kursor" czytania pliku catalog.dat właśnie na ten wiersz.
Nazwa: fseek
W zasięgu deklaracji z poprzedniego przykładu kodu, instrukcje:
/* ... */
fseek(f,208*1111,SEEK_SET);
fgets(buff,210,f);
sscanf(buff+13,"%c",&znak);
if(znak != 'X')
{
sscanf(buff," %d %d %d",&tyc1, &tyc2, &tyc3);
sscanf(buff+15," %lf",&alfa);
sscanf(buff+28," %lf",&delta);
}
/* .... */
przeczyta dane nie z pierwszego wiersza katalogu tylko dane dotyczące pierwszej gwiazdy z 1111 pola GSC.
A skąd wiadomo, które pola GSC nas interesują ?
Wracamy tu do definicji naszego zadania. Będziemy tworzyli histogramy gęstości polowej gwiazd wzdłuż południkowych lub równoleżnikowych "pasków" na sferze, zawsze o szerokości 2° .
Uwaga! Niezależnie od typu "paska" POMIJAMY okolice okołobiegunowe, ignorując paski lub gwiazdy pojawiające sie bliżej biegunów niż 2° w deklinacji. Pracujemy więc w całym zadaniu na zakresie deklinacji od -88° do +88°.
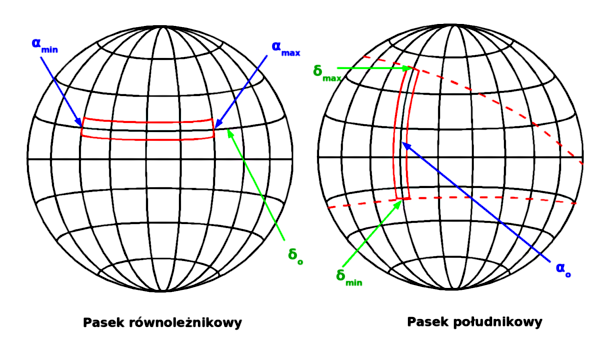
Rysunek 2.
Pasek południkowy użytkownik programu definiuje poprzez podanie rektascencji αo środkowego południka (z zakresu od 0h do 24h, w postaci godzin, minut i sekund czasowych z ułamkiem) oraz minimalnej (δmin ) i maksymalnej (δmax ) deklinacji branych pod uwagę gwiazd (z zakresu od -88° do +88° w postaci stopni ze znakiem, minut i sekund z ułamkiem).
Pasek równoleżnikowy użytkownik programu definiuje poprzez podanie deklinacji δo środkowego równoleżnika (z zakresu od -88° do +88° w postaci stopni ze znakiem, minut i sekund z ułamkiem) oraz minimalnej (αmin ) i maksymalnej (αmax ) rektascencji branych pod uwagę gwiazd (z zakresu od 0h do 24h, w postaci godzin, minut i sekund czasowych z ułamkiem).
W obu przypadkach zakresy (δmin , δmax ) oraz (αmin , αmax ) są umieszczane odpowiednio na środkowym południku lub równoleżniku paska a końce paska tworzone są z łuków kół wielkich o długości 2°, przechodzących prostopadle do paska przez wskazane punkty. Konstrukcję "pasków" ilustruje Rysunek 2.
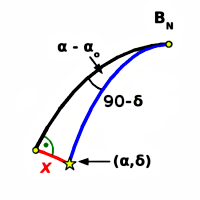
Rysunek 3.
Aby ustalić czy jakiś punkt o współrzędnych (α,δ) należy do naszego paska trzeba wyliczyć jego odległość od centralnego równoleżnika lub południka wzdłuż prostopadłego koła wielkiego i sprawdzić, czy odległość ta jest mniejsza od 1°.
Dla paska równoleżnikowego sprawa jest prosta i sprowadza się do sprawdzenia różnic współrzędnych równikowych.
W przypadku paska południkowego należy każdorazowo wyliczyć odległość x z prostokątnego trójkąta sferycznego pokazanego na Rysunku 3.
Jeśli zauważymy, że z warunków zadania wynika, iż x jest zawsze małe, a na pewno mniejsze od 90°, to wystarczy skorzystać z twierdzenia sinusów dla pokazanego na Rysunku 3 trójkąta sferycznego by otrzymać:
sin(x) = cos(δ)·sin(α - αo)
Skoro umiemy już rozstrzygnąć, czy punkt o współrzędnych (α,δ) należy do naszego "paska" to skorzystajmy w pełni z pliku indeksowego.

Format tego pliku opisany jest w Tabeli 4. Powtórzmy: n-ty wiersz pliku index.dat w pierwszej kolumnie zawiera numer wiersza z pliku catalog.dat, w którym zaczynają się gwiazdy n-tego pola GSC (TYC1).
A skąd mamy wiedzieć, czy dane pole GSC nas interesuje? O tym decydują dalsze informacje z tego samego wiersza: kolumnę drugą pomijamy a kolumny od 3 do 6 zawierają odpowiednio najmniejszą i największą rektascencję i deklinację gwiazd występujących w danym polu, zgodnie z opisem w Tabeli 4.
Wszystkie cztery liczby zapisane są w stopniach z dwoma cyframi po przecinku (deklinację może poprzedzać minus).
Poniżej mamy pokazane kilka pierwszych i kilka ostatnich wierszy z pliku index.dat:
1| 1| 0.00| 2.49| 0.00| 2.49
168| 1| 2.50| 5.00| 0.00| 2.50
341| 5| 5.00| 7.49| 0.04| 2.50
497| 5| 0.00| 2.49| 2.50| 5.00
705| 7| 2.51| 5.00| 2.52| 4.99
873| 9| 5.00| 7.50| 2.52| 4.98
1026| 9| 0.01| 2.50| 5.00| 7.48
.
.
.
2539704| 17589|241.48|269.63|-89.87|-88.17
2539757| 17589|270.62|298.55|-89.67|-88.17
2539806| 17589|300.13|329.48|-89.71|-88.13
2539865| 17589|330.85|359.50|-89.70|-88.14
2539914| 17589| 0.00| 0.00| 0.00| 0.00
Z trzeciego wiersza wynika np., że trzecie pole GSC zaczyna się w 341 wierszu pliku catalog.dat, a zawarte w tym polu gwiazdy mają rektascencje z przedziału od 2.5 do 5 stopni a deklinacje od 0 do 2.5 stopni. Wiedząc gdzie użytkownik naszego programu umieścił badany pasek sfery niebieskiej potrafimy na podstawie tych danych jednoznacznie rozstrzygnąć, czy to pole GSC dotyka choćby naszego paska, czy też jest całkowicie do pominięcia, bo żadna znajdująca się w nim gwiazda nie może znaleźć się w pasku.
Jak dotąd struktura naszego programu wygląda następująco:
- Pytamy użytkownika czy chce badać pasek równoleżnikowy czy południkowy.
- Pobieramy dane definiujące położenie wybranego paska.
- Kopiujemy do odpowiednio zadeklarowanej tablicy te wiersze katalogu Tycho-2, które opisują gwiazdy na pasku. W tym celu:
- Otwieramy pliki index.dat oraz catalog.dat .
- Czytamy kolejno wiersze pliku index.dat i decydujemy, czy opisywane pole GSC zahacza o nasz pasek.
- Jeśli tak, skaczemy do odpowiedniego wiersza pliku catalog.dat (funkcją fseek() opisaną wyżej) i czytamy kolejno wiersze opisujące każdą gwiazdę pola, kopiując do tablicy tylko te, które opisują gwiazdy z paska.
- Jeśli nie to pomijamy o pole GSC i czytamy następny wiersz pliku index.dat .
- Gdy dojdziemy do końca pliku index.dat (ma on specjalną zawartość co widać wyżej) mamy przejrzany cały katalog Tycho-2 i skopiowane dane opisujące wszystkie gwiazdy tego katalogu leżące na badanym pasku. Nie zapomnijmy w tym miejscu zamknąć plików index.dat oraz catalog.dat .
Kilka słów komentarza: jak zadeklarować tablicę na kopiowane wiersze katalogu i jak te wiersze umieszczać w tablicy.
Oto podpowiedź:
/* użycie niżej funkcji kopiowania łańcuchów znaków strcpy()
wymaga nowego pliku nagłówkowego: */
#include<string.h>
/* na początku kodu definiujemy maksymalną liczbę obsługiwanych gwiazd.
W czasie testowania programu może to być np. 1000 albo 10000
do zaliczenia przystępujemy z definicją: */
#define MAX (100000)
/* korzystając z tej definicji deklarujemy w programie tablicę: */
char A[MAX][210];
/* tablica ta pomieści MAX wierszy po 210 znaków (lekki zapas nie zaszkodzi) */
/* jeśli teraz w zmiennej pole mamy numer pola GSC to: */
fseek(f,208*pole,SEEK_SET); /* skacze do odpowiedniego wiersza katalogu */
k=0; /* k zerujemy tylko przed czytaniem pierwszego pola ! */
while(fgets(buff,300,f) != NULL) /* dopóki są dane */
{
sscanf(buff," %d",&tyc1);
if(tyc1 != pole) break; /* koniec gwiazd tego pola */
sscanf(buff+13,"%c",&znak);
if(znak != 'X')
{
strcpy(A[k++],buff); /* kopiujemy cały buff (wiersz katalogu)
do k-tego wiersza tablicy A[][] */
/* Można to zapisać bardziej czytelnie :
strcpy(&A[k++][0],buff);
co daje identyczny rezultat */
}
else continue; /* wiersz bez danych */
if(k==MAX) break; /* zapełniona tablica */
}
/* .... */
Na pracowni w katalogu /home/COMMON/dydaktyka/III_rok_astronomii/programowanie/ jest mój program o nazwie tycho_test, który realizuje opisane wyżej czynności, podając na końcu ile gwiazd z katalogu Tycho-2 pobrał. Mój program dodatkowo sortuje wybrane gwiazdy i wypisuje pierwsze i ostatnie dziesięć sztuk. To Państwa czeka w następnym etapie, a potem już tylko histogram gęstości polowej wykonany biblioteką PGPLOT.
Proszę potraktować powyższy opis jako pierwszą część zadania i zacząć pisać program wybierający poprawnie tyle samo gwiazd.
Na tym etapie proszę koniecznie przeczytać i usilnie spróbować zrozumieć Rozdział 5 "Wskaźniki i tablice" z podręcznika Kernighana & Ritchie-go!
Można pominąć podrozdziały: 5.10, 5.11 i 5.12. ![]()
Po przestudiowaniu podręcznika proszę sprawdzić swoją wiedzę czytając ten materiał
Co dalej?
Teraz mając wybrane i skopiowane do tablicy wiersze interesujących nas gwiazd należy je posortować wzdłuż "paska" czyli pasek południkowy według deklinacji a równoleżnikowy według rektascencji.
Stosować będziemy najprostszy chyba algorytm sortowania, tzw. sortowanie bąbelkowe. Ładny materiał na ten temat można znaleźć pod adresem: http://www.home.umk.pl/~abak/wdimat/s/BubbleSort.html .
Warto pobawić się zawartym tam apletem by oswoić się z działaniem tego algorytmu.
A po co uczyliśmy się o wskaźnikach (pointerach)?
Otóż sortowania nie będziemy realizować przestawiając zgodnie z algorytmem "bąbelkowym" całych wierszy tablicy zawierającej kopie fragmentu katalogu. Zamiast tego stworzymy tablicę wskaźników do wierszy tej pierwszej tablicy i sortować będziemy przestawiając jedynie wskaźniki!
Poniższy kod pokazuje jak zadeklarować tablice A i B oraz jak tę ostatnią zainicjować:
#define MAX (100000)
char A[MAX][210];
char * B[MAX];
/* ... tu wybieramy gwiazdy i wstawiamy wiersze do tablicy A[][]... */
for(i=0;i<MAX;++i) B[i] = &A[i][0];
/* lub krócej ale mniej czytelnie:
for(i=0;i<MAX;++i) B[i] = A[i]; */
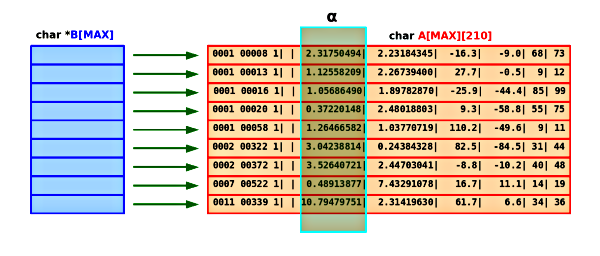
Rys.4. Tablice przed sortowaniem.
W ten sposób pierwszy element tablicy B[] wskazuje PRZED SORTOWANIEM na pierwszy znak pierwszego wiersza tablicy A[][], drugi na pierwszy znak drugiego itd., jak to pokazano na Rysunku 4.
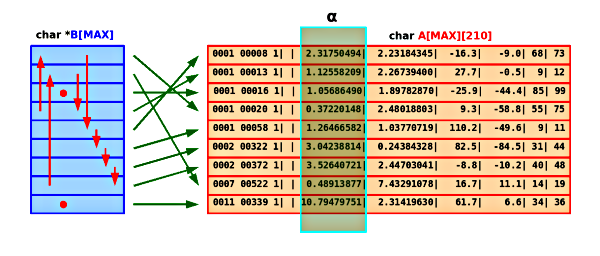
Rys.5. Tablice po sortowaniu.
Jeśli założyć, że sortujemy rosnąco według rektascencji (wyróżniona kolumna na rysunkach 4 i 5) to po sortowaniu elementy tablicy B[] powinny wskazywać początki wierszy tablicy A[][] jak na Rysunku 5.
Zamiast "miotać" ponad dwustu-bajtowymi wierszami tablicy A[][] przemieszczamy jedynie kilku-bajtowe elementy tablicy B[] (czerwone strzałki na Rys.5.).
Ale jak sortować elementy tablicy B[]?
Przecież porównywanie zawartych w nich wskaźników (pointerów, adresów) nie ma sensu!!
Mamy posortować gwiazdy wzdłuż paska, rosnąco lub malejąco, jak nam wygodniej będzie potem, przy robieniu histogramu. Czyli o ewentualnej zamianie elementów tablicy B[] musi decydować odpowiednia współrzędna równikowa gwiazdy, której wiersz jest wskazywany przez dany element tablicy B[] !
Podpowiedź jak to zrobić jest w poniższym kawałku kodu. Korzystamy tu z poznanej wyżej funkcji sscanf() . Jeśli, jak na rysunkach 4 i 5, sortujemy malejąco według rektascencji, to decyzja, czy zamienić elementy B[i] oraz B[i+1] wymaga czegoś w rodzaju:
char * zapas;
/* magiczna liczba 15 poniżej wynika z faktu, że czytamy rektascencję.
Dla deklinacji byłoby to 28 */
sscanf(B[i]+ 15," %lf",&alfa1);
sscanf(B[i+1]+ 15," %lf",&alfa2);
if(alfa1>alfa2) {
zapas = B[i];
B[i] = B[i+1];
B[i+1] = zapas;
}
Zwracam uwagę, że tylko przy porównywaniu elementów B[0] oraz B[1] musimy dwa razy wywołać (bardzo czasochłonną!) funkcję sscanf(). Przy każdym następnym porównaniu pierwszą rektascencję mamy już przeczytaną proszę więc tak zorganizować program by z tego faktu skorzystać. Obowiązkowo.
Skoro umiemy "porównać" dwa kolejne elementy tablicy B[] i wcześniej poznaliśmy (i przećwiczyli) algorytm sortowania bąbelkowego, to na tym etapie nasz program ma już gwiazdy posortowane. Czytanie skopiowanych z katalogu wierszy według kolejności zapisanej w tablicy B[] dostarczy nam właśnie posortowanych danych o gwiazdach.
Teraz już tylko histogram
Umawiamy się "na sztywno", że całą długość "paska" dzielimy na 50 podprzedziałów, liczymy ile gwiazd jest w każdym podprzedziale i rysujemy (biblioteką PGPLOT) histogram malując 50 prostokątów o wysokości proporcjonalnej do wyznaczonej liczby gwiazd.
Jako minimum, można skorzystać z gotowej funkcji cpgbin(), co ilustruje bardzo zgrubnie poniższy przykład:
/*****************************************************************************
**** histogram.c ****
******************************************************************************
**** ****
**** Symulacja rysowania histogramu.... ****
**** Przykład użycia funkcji cpgbin() z biblioteki PGPLOT ****
**** ****
**** ****
******************************************************************************
**** Created by PAD, last modified: 27-12-2008 ****
*****************************************************************************/
#include <stdio.h>
#include <cpgplot.h>
int main(void)
{
int k;
float data[50]={ 0.0, 0.0, 10.0, 12.0, 13.0, 16.0, 18.0, 20.0, 28.0, 45.0,
67.0, 89.0, 88.0, 76.0, 70.0, 54.0, 51.0, 43.0, 38.0, 23.0,
20.0, 26.0, 29.0, 13.0, 11.0, 0.0, 0.0, 10.0, 12.0, 13.0,
16.0, 18.0, 20.0, 28.0, 45.0, 67.0, 89.0, 88.0, 76.0, 70.0,
54.0, 51.0, 43.0, 38.0, 23.0, 20.0, 26.0, 29.0, 13.0, 11.0 };
float x[50] ={ 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9,
1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9,
2.0, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9,
3.0, 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9,
4.0, 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9 };
k=cpgopen("?");
if(k!=1) {
puts("\n\ncpgopen error\n");
return 0;
}
cpgslw(4);
cpgenv(0,5,0,100,0,-1);
cpgbin(50,x,data,0);
cpgclos();
}
Rys.6. Wynik działania powyższego kodu.
Uzyskanie jednak akceptowalnego rysunku wymaga trochę więcej pracy, np. osie mają być opisane!
Wysokość rysunku ma być dynamicznie dopasowana do wysokości najwyższego słupka histogramu, np. 115% tej wysokości.
No i opis osi poziomej, odpowiadającej deklinacji lub rektascencji gwiazd, ma być "porządny i ładny". Czyli np. od 22h przez 0h do 3h !
Raczej zachęcam do "ręcznego" skomponowania histogramu z odpowiednio ładnie (i może kolorowo) wypełnionych prostokątów oraz "ręcznie" poumieszczanych opisów.
I to wszystko!



