Autorem poniższego opracowania jest dr Piotr A. Dybczyński z Instytutu Obserwatorium Astronomiczne UAM w Poznaniu.
Metoda Monte-Carlo : zadania do wyboru
Zadanie polega na wyznaczeniu metodą Monte-Carlo pola wybranej figury z dokładnością trzech cyfr znaczących.
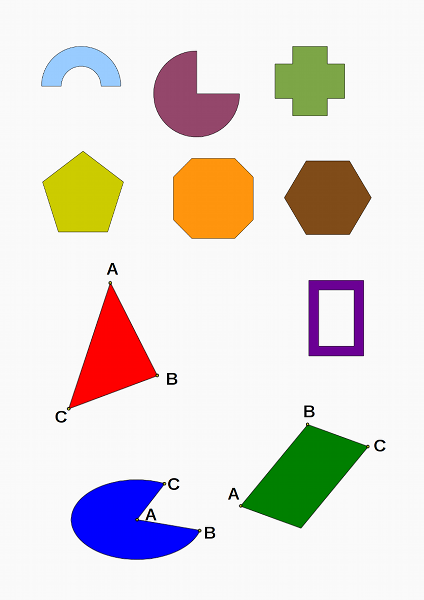
Figury do wyboru.
- Połowa pierścienia z dwóch kół - zdefiniowanego przez dwa promienie, (2)
- Koło w wyciętą ćwiartką, jeden parametr: promień, (3)
- Krzyż powstały z kwadratu po wycięciu czterech mniejszych kwadratów, dwa parametry, boki obu kwadratów, (6)
- Pięciokąt foremny, jeden parametr: bok, (7)
- Ośmiokąt powstały z kwadratu po odcięciu czterech równych narożników, dwa parametry: bok kwadratu i przyprostokątna odciętego trójkąta, (6)
- Szeciokąt foremny, jeden parametr: bok, (5)
- Dowolny trójkąt zdefiniowany przez podanie współrzędnych trzech wierzchołków, (7)
- Prostokątna ramka o równej szerokości, trzy parametry, wymiary zewnętrzne i szerokość ramki, (4)
- Wycinek elipsy zdefiniowany przez środek (A) oraz dwa punkty na krawędzi elipsy (B i C), (10)
- Ukośny równoległobok zdefiniowany przez trzy wierzchołki A, B i C (7)
W nawiasach na czerwono podano szacunkową trudność zadania w skali od 1 do 10.

