V . PRAWDOPODOBIEŃSTWO POWSTANIA ORBITY OBSERWOWALNEJ.
Na zakończenie rozważań o wpływie przejścia gwiazdy na orbitę komety z obłoku Oorta przedstawimy przykłady oszacowania prawdopodobieństwa powstania orbity obserwowalnej. Tak jak poprzednio, rozważamy jedynie skutki pojedynczego przejścia gwiazdy.
Zanim przystąpimy do prezentacji wyników dla całego obłoku kometarnego opiszemy stosowane w tym rozdziale metody na przykładzie zagadnienia płaskiego.
PRZYKŁAD SYMULACJI DLA ZAGADNIENIA PŁASKIEGO.
Weźmy na początek kometę o ustalonej orbicie nieperturbowanej, opisanej następującym zestawem elementów, odniesionych jak poprzednio do układu OXYZ związanego z płaszczyzną ruchu gwiazdy:
Q∈ = 100000 AU, q∈ = 10000 AU, i∈ = 0° , Ω∈ = 0° , ω∈ = 220° , M∈ z przedziału <0°,360°) ,
Badać będziemy w tym przykładzie oddziaływanie gwiazdy o następujących parametrach:
V∞ = 10 km/s, M* = 5 Mo, bo = 50000 AU.
Gwiazda ta przecina orbitę komety w dwóch punktach, opisanych anomalią średnią równą ok. 133° i 321° .
Zależność zmiany odległości perihelium komety od anomalii średniej punktu największego zbliżenia z gwiazdą przedstawiamy na rysunku 5.1.
Rys. 5.1. Przebieg zmian q∈ dla omawianego przykładu.
Zrezygnowaliśmy na rysunku 5.1 z jednoczesnego pokazania wyników całkowania numerycznego, ponieważ zamazałoby to obraz zależności. Na rysunku widać dwa przedziały M∈ , w których q∈ spada do zera.
'''Jeżeli będziemy wybierali losowo pozycję komety w dowolnej chwili czasu i realizowali dla tego momentu przelot gwiazdy o zadanych parametrach a następnie badali czy q∈ po przejściu gwiazdy jest mniejsze od 10 AU, to dla wystarczająco dużej próby komet możemy oszacować prawdopodobieństwo powstania orbity obserwowalnej'''. Z liniowej zależności anomalii średniej od czasu wynika, że zamiast wybierać losowo moment czasu, wystarczy losować wartość M∈ z przedziału <0°,360°) pod warunkiem, że wszystkie wartości będą równo prawdopodobne.
Zanim jednak przedstawimy wyniki takiej symulacji oszacujemy szukane prawdopodobieństwo wprost z rysunku. Wystarczy bowiem znaleźć sumę długości tych przedziałów anomalii średniej, dla których krzywa opada poniżej granicy 10 AU a następnie obliczyć stosunek otrzymanej wartości do długości całego przedziału zmienności M∈ .
W tym celu wykreślimy ponownie, w znacznie większej skali te fragmenty krzywej z rysunku 5.1 , dla których q∈ < 10 AU .
Rysunki 5.2 i 5.3 przedstawiają właśnie te fragmenty, uzyskane metodą impulsową ( linia ciągła ) i całkowaniem numerycznym ( punkty ). Na obu wykresach ciągła, pozioma linia oznacza granicę 10 AU.
Jeśli przyjrzymy się dokładnie rysunkowi 5.1 to zauważymy, że poza przedziałami pokazanymi na rysunkach 5.2 i 5.3 odległość perihelium komety spada do zera jeszcze w dwóch miejscach. Leżą one w bezpośrednim sąsiedztwie punktów przecięcia orbity komety przez gwiazdę. Szczegółowe rachunki, wykonane tak przy użyciu metody impulsowej, jak i całkowania numerycznego pokazują, że wymienione obszary mają rzeczywiście charakter punktowy i długość równą zeru na poziomie dokładności komputera.
Cecha ta znalazła potwierdzenie w dużej ilości testowych przypadków przecinania orbity komety przez gwiazdę i pozwala ograniczyć rozważanie naszego przykładu tylko do przedziałów z rysunków 5.2 i 5.3 .
Rys 5.2. Pierwszy przedział redukcji q∈ poniżej 10 AU .
Rys 5.3. Drugi przedział redukcji q∈ poniżej 10 AU .
Wyznaczenie na tych rysunkach przybliżonej długości interesujących nas przedziałów nie nastręcza trudności. Odczytana z rysunku długość pierwszego przedziału wynosi w przybliżeniu 7.93° , natomiast długość drugiego przedziału: 0.56° .
Po zsumowaniu i podzieleniu przez 360° otrzymujemy przybliżoną wartość szukanego prawdopodobieństwa p powstania orbity obserwowalnej w naszym przykładzie:
p ≅ 0.0236.
Na rysunkach 5.2 i 5.3 pokazano również wyniki całkowania numerycznego. Dzięki dużej skali rysunków widać wyraźnie niewielkie przesunięcie tych wyników w stosunku do krzywej otrzymanej metodą impulsową. Można sprawdzić, że przesunięcie to nie zmienia ( na poziomie dokładności tych rozważań ) długości przedziału anomalii średniej, w którym q∈ < 10 AU . Jest to również prawidłowość potwierdzona szeregiem przebadanych przypadków.
Przesunięcie wyników całkowania numerycznego w stosunku do rezultatów metody impulsowej jest zwykle znacznie mniejsze, ponieważ w omawianym przykładzie gwiazda ma masę największą z rozważanych i stosunkowo małą prędkość. Dodatkowym potwierdzeniem stosowalności metody impulsowej w takich zagadnieniach są przedstawione dalej wyniki rachunków symulacyjnych.
Opiszemy jednak najpierw zastosowaną w nich metodę obliczania prawdopodobieństwa na podstawie wyników losowania. Nasze postępowanie możemy potraktować jako szukanie nieznanego prawdopodobieństwa zdarzenia A , w tym przypadku zdefiniowanego następująco: kometa o wylosowanej anomalii średniej zmienia orbitę na obserwowalną pod wpływem przelotu gwiazdy. Jeżeli ilość losowań jest dostatecznie duża to prawdopodobieństwo p zdarzenia A można oszacować jako stosunek ilości wystąpień tego zdarzenia do całkowitej liczby losowań.
Nawet dla bardzo dużych liczebności prób wyliczone tą metodą prawdopodobieństwo jest jednak obarczone pewnym błędem. Posłużymy się więc znaną metodą wyznaczania przedziału ufności dla nieznanego prawdopodobieństwa ( por.np. Smirnow i Dunin-Barkowski, 1973, str. 174 i nast. ).
Aby uzyskać wyniki jak najbardziej wiarygodne przyjęliśmy w tej pracy często używane tzw. kryterium "3σ" , co oznacza że będziemy wyznaczać przedział ufności o długości 6σ , gdzie σ oznacza odchylenie standardowe otrzymanego wyniku.
Prawdziwa wartość szukanej wielkości znajduje się w takim przedziale z prawdopodobieństwem 99.7 % .
Jeżeli przez n oznaczymy liczbę wszystkich losowań, przez k liczbę "sukcesów" czyli wystąpień zdarzenia A oraz przez t połowę długości przedziału ufności wynikającą z przyjętego kryterium i wyrażoną w jednostkach równych σ , to w oparciu o formuły z cytowanej wyżej pracy możemy szukane prawdopodobieństwo zdarzenia Aprzedstawić jako:
(5.1)
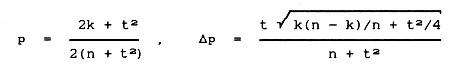
Ponieważ w naszym przypadku t = 3 (kryterium "3σ") to po podstawieniu tej wartości do powyższych wzorów otrzymujemy ostatecznie:
(5.2)
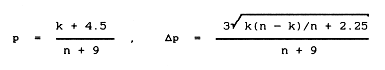
Dla omawianego przykładowego przelotu gwiazdy przeprowadziliśmy dwa rachunki symulacyjne według opisanego wcześniej schematu.
W jednym stosowaliśmy pełną metodę impulsową, w drugim każdorazowo całkowaliśmy numerycznie równania ruchu komety. W obu przy padkach liczba wszystkich losowań wynosiła: n = 73389.
Stosując całkowanie numeryczne otrzymaliśmy z tej próby 1689 orbit obserwowalnych,co daje:
p = 0.0231 )+ 0.0016,
natomiast stosując metodę impulsową otrzymaliśmy 1705 orbit obserwowalnych, czyli w tym przypadku:
p = 0.0233 )+ 0.0017.
Należy zaznaczyć, że losowanie w pierwszej symulacji było całkowicie niezależne od losowania w drugiej, tak więc różnica w ilości otrzymanych orbit obserwowalnych jest typową fluktuacją statystyczną, co znajduje pełne potwierdzenie w bardzo dobrej zgodność otrzymanych prawdopodobieństw. Widać też zgodność z przybliżoną wartością prawdopodobieństwa, otrzymaną wprost z rysunków.
Oczywiście taka symulacja, w której ustalone są elementy orbity komety niewiele mówi nam o prawdopodobieństwie powstania orbity obserwowalnej na skutek przejścia gwiazdy o zadanych parametrach ruchu przez cały obłok wypełniony kometami na orbitach o dowolnej orientacji płaszczyzny ruchu i linii absyd, oraz o zmieniających się w pewnych granicach Q)j i q)j . Przykład ten miał za zadanie umożliwić zaprezentowanie stosowanej metody rachunków symulacyjnych , niezależnej od metody wyznaczania zmian orbity komety. Drugim ważnym celem było pokazanie, że metoda impulsowa w pełni nadaje się do tego typu rachunków. O wadze tego drugiego wniosku niech powiedzą następujące dane: stosując całkowanie numeryczne możemy wyliczyć skutki przejścia gwiazdy dla 1500 komet w ciągu godziny pracy komputera, w tym samym czasie metoda impulsowa pozwala otrzymać wyniki dla 750000 komet.
Przybliżenie impulsowe daje więc rezultaty 500 razy szybciej !
W następnych rachunkach symulacyjnych stosować więc będziemy wyłącznie metodę impulsową ponieważ będą one dotyczyć całego obłoku kometarnego i dla oszacowania szukanego prawdopodobieństwa trzeba testować populacje komet o liczebności dziesiątek milionów.
Zanim przystąpimy do wspomnianych rachunków przedstawimy jeszcze wyniki czterech symulacji w zagadnieniu płaskim o wszystkich parametrach identycznych z podanymi na początku rozdziału. Wprowadzimy jedynie losową orientację linii absyd, czyli oprócz anomalii średniej losować będziemy również argument perihelium.
W czterech niezależnych rachunkach stopniowo zwiększaliśmy liczebność testowanej populacji komet, aby pokazać jak dokładność otrzymywanego prawdopodobieństwa zmienia się z tą liczebnością. Wyniki zebraliśmy w Tabeli 10.
Tabela 10. Wyniki czterech symulacji w przypadku płaskim.
1 n $1 k $1 p $1 Dp $1
j--------------k---------------k----------------k----------------l
1 100000 $1 352 $1 0.003565 $1 0.000564 $1
1 200000 $1 674 $1 0.003392 $1 0.000389 $1
1 300000 $1 987 $1 0.003305 $1 0.000314 $1
1 1000000 $1 3340 $1 0.003344 $1 0.000173 $1
m--------------,---------------,----------------,----------------.
Otrzymane prawdopodobieństwa są prawie o rząd mniejsze od wartości uzyskanej poprzednio ponieważ przyjęta w pierwszej symulacji stała wartość argumentu perihelium, równa 220 , opisywała konfigurację geometryczną sprzyjającą powstawaniu orbit obserwowalnych. Dla niektórych innych wartości powstanie takiej orbity w wyniku przelotu gwiazdy o podanych parametrach nie jest możliwe.
SYMULACJA PRZEJSCIA GWIAZDY PRZEZ OBŁOK OORTA.
Zajmiemy się teraz symulacją numeryczną przejścia gwiazdy o zadanych parametrach M , V)h i b)g przez obłok kometarny. Stosujemy metody przedstawione w poprzednim paragrafie z tą różnicą, że wszystkie elementy orbity komety przyjmują wartości losowe w pewnych przedziałach zmienności.
Dla równomiernego rozkładu orientacji płaszczyzn ruchu i linii absyd komet w obłoku ( por Yabushita, 1972, str. 401 ) wyznaczamy wartości W)j, w)j oraz cos i)j przy pomocy generatora liczb losowych o rozkładzie jednostajnym na przedziale <0,1) ,mnożąc otrzymywane liczby pseudolosowe przez odpowiednie współczynniki aby aby otrzymać następujące przedziały zmienności tych elementów:
Również anomalia średnia komety ma rozkład jednostajny na przedziale <0 ,360 ). Pozostaje nam określić, w jaki sposób otrzymywaliśmy wartości Q)j i q)j . W literaturze przedmiotu znaleźć można najróżniejsze, proponowane rozkłady prawdopodobieństwa dla tych elementów, począwszy od stałych wartości wielkiej półosi lub mimośrodu dla wszystkich komet w obłoku, a skończywszy na złożonych rozkładach wynikających z przyjętej hipotezy powstania obłoku kometarnego, por. np. : Yabushita i inni 1982, Weissman 1984, Remy i Mignard 1985, Staniucha i Banaszkiewicz 1988.
Dlatego w przedstawionych przykładach szacowania prawdopodobieństwa powstania orbit obserwowalnych nie chcąc ograniczać się do wartości stałych przyjęliśmy schemat możliwie najprostszy:
Q)j e < 1)W1094 AU, 1)W1095 AU>, q)j e < 1)W1093 AU, Q)j>,
przy czym w obu przypadkach rozkład wartości w podanym przedziale jest jednostajny. Oczywiście najpierw losujemy Q)j , potrzebne do określenia przedziału zmienności q)j . Wynikające z takiego schematu przykładowe rozkłady wielkiej półosi i mimośrodu dla populacji 25000 komet przedstawiamy na Rys. 5.4 i 5.5.
Rys. 5.4. Przykładowy rozkład wielkiej półosi orbit komet dla przyjętego modelu obłoku kometarnego.
Należy podkreślić, że taki wybór modelu obłoku kometarnego znajduje niewątpliwie swoje odbicie w otrzymanych rezultatach. Dla istotnie różnych modeli, wartości otrzymanych prawdopodobieństw mogą odbiegać od wyników podanych w tej pracy. Ponieważ jednak nie jest znany prawdziwy rozkład elementów orbit komet w obłoku Oorta ( samo istnienie tego obłoku jest wciąż przecież dyskutowane ), przyjęcie takiego arbitralnego rozstrzygnięcia dla rachunków symulacyjnych wydaje się dopuszczalne. Należałoby niewątpliwie w przy szłości przeprowadzić podobne badania dla innych modeli.
Rys.5.5. Przykładowy rozkład mimośrodu orbit komet dla przyjętego modelu obłoku kometarnego
Z rysunków 5.4 i 5.5 wynika między innymi,że w przyjętym modelu obłoku kometarnego występuje przewaga orbit o mniejszych mimośrodach, rozkład wielkich półosi jest w przedziale od 1)W1094 AU do 5)W1094 AU w przybliżeniu jednostajny, większe wartości a)j są mniej prawdopodobne.
W pierwszej symulacji przelotu gwiazdy przez obłok kometarny przyjęliśmy następujące wartości parametrów jej ruchu:
M = 1 M)g,
V)h = 20 km/s,
b)g = 30000 AU.
Oprócz podstawowego rachunku dla całego obłoku przeprowadziliśmy jeszcze szereg symulacji dla podzbiorów komet o stałych wartościach Q)j i q)j . Pozwala to ocenić, jak szukane prawdopodobieństwo zależy od wyboru tych elementów a jednocześnie uwalnia te wyniki od wpływu przyjętego rozkładu Q)j i q)j .
Otrzymane wyniki zebraliśmy w poniższej tabeli.
Tabela 11. Wyniki symulacji numerycznej dla przejścia gwiazdy
o parametrach: M = 1 M)g, V)h = 20km/s, b)g = 30000 AU.
a=========s============s============s=============s=============d
2 100000 $2 2.26)W109-5 $2 3.26)W109-7 $2 5.62)W109-7 $2 2 2 AU $2 )+0.37)W109-5 $2 )+1.99)W109-7 $2 )+4.19)W109-7 $2 < 5)W109-8 $2
a=========s============s============s=============s=============d
2 80000 $2 2.12)W109-5 $2 3.62)W109-7 $2 2 2 2 AU $2 )+0.42)W109-5 $2 )+2.09)W109-7 $2 < 5)W109-8 $2 2
a=========s============s============s=============c 2
2 40000 $2 1.80)W109-5 $2 3.65)W109-7 $2 2 2 AU $2 )+0.42)W109-5 $2 )+2.03)W109-7 $2 2
2 10000 $2 2 3.07)W109-7 )+ 1.76)W109-7 $2 z=========x============x========================================c
Widzimy, że prawdopodobieństwo powstania orbity obserwowalnej jest wyraźnie większe dla orbit o małej, początkowej wartości q)j . Dla orbity o Q)j = 10000 AU gwiazda przechodzi za daleko aby wywołać pożądaną zmianę q)j . Duża niepewność większości pokazanych wartości wynika z tego, że dla populacji komet rzędu 20 mln. otrzymywaliśmy tylko po kilkanaście orbit obserwowalnych.
W tych przypadkach, w których podajemy tylko górną granicę wyniku nie otrzymaliśmy z populacji 20 mln. komet ani jednej takiej orbity, jednak z wartości Q)j dla tych orbit wynika, że szukane prawdopodobieństwo jest niezerowe.
Otrzymane wartości są pozornie bardzo małe, jednak gdy uświadomimy sobie szacowaną liczebność obłoku kometarnego , rzędu 10912, to powstanie wielu orbit obserwowalnych w czasie jednego przelotu gwiazdy wydaje się całkiem realne.
Aby przedstawić maksimum informacji o warunkach sprzyjających powstaniu orbity obserwowalnej pokażemy jeszcze dla orbit komet o początkowym Q)j = 100000 AU i q)j = 1000 AU rozkłady tych wartości czterech losowanych elementów kątowych, dla których orbita powyższa przechodziła w obserwowalną. Spośród 6.4 mln. wylosowanych komet o podanych wartościach odległości aphelium i perihelium tylko 159 doznało takiej zmiany orbity, że mogłyby być zaobserwowane. Rozkłady początkowych wartości W)j, w)j, i)j oraz M)j dla tych 159 komet przedstawiają rysunki 5.6, 5.7, 5.8 i 5.9.
Rys. 5.6. Rozkład początkowego nachylenia dla komet, których q)j zmniejszyło się poniżej 10 AU.
Rys. 5.7. Rozkład początkowej anomalii średniej komet, których q)j zmniejszyło się poniżej 10 AU.
Rys. 5.8. Rozkład długości węzła wstępującego dla komet, których q)j zmniejszyło się poniżej 10 AU.
Rys. 5.9. Rozkład argumentu perihelium dla komet, których q)j zmniejszyło się poniżej 10 AU.
Widoczne na powyższych rysunkach rozkłady W)j i w)j wykazują silną koncentrację tych elementów wokół wartości opisujących konfiguracje sprzyjające powstaniu orbity obserwowalnej.
Dla wymienionych, początkowych wartości Q)j i q)j orbity obserwowalne powstają najczęściej gdy linia absyd orbity wyjściowej tworzy z torem gwiazdy kąt ok. 20 .
Rozkłady M)j i i)j są raczej równomierne, pomijając niewystępowanie anomalii średniej, opisującej bezpośrednie otoczenie peri helium.
Na koniec przedstawimy rezultaty jeszcze jednej symulacji, dla masywniejszej i wolniejszej gwiazdy, przechodzącej jednak znacznie dalej od Słońca.
Tabela 12. Wyniki symulacji numerycznej dla przejścia gwiazdy
o parametrach: M = 2 M)g, V)h = 10km/s, b)g = 90000 AU.
a=========s============s============s=============s=============d
2 100000 $2 1.85)W109-4 $2 3.92)W109-6 $2 4.45)W109-7 $2 3.58)W109-7 $2 2 AU $2 )+0.41)W109-4 $2 )+2.30)W109-6 $2 )+2.06)W109-7 $2 )+1.84)W109-7 $2
a=========s============s============s=============s=============d
2 80000 $2 4.35)W109-5 $2 2 2 2 a=========s============s============s=============c 2
2 40000 $2 2 2 2 2 10000 $2 2 3.58)W109-7 )+ 1.84)W109-7 $2 z=========x============x========================================c
Pomimo istotnej zmiany parametrów ruchu gwiazdy, prawdopodobieństwo uzyskane z globalnej symulacji dla całego obłoku ma wartość zbliżoną do poprzedniej. W obu rachunkach populacja testowanych komet przekracza 100 mln.
W pracy Yabushita i inni, 1982, omawianej w rozdziale trzecim autorzy przeprowadzili podobne do naszych, symulacyjne badania wpływu przypadkowych przejść gwiazdowych na elementy orbit komet blisko-parabolicznych. Autorzy nie przeprowadzili rachunków dla całego obłoku kometarnego,ograniczając sie do sześciu typów orbit: trzy orbity eliptyczne o a)j = 25000 AU i q)j równym 1, 5 i 10 AU oraz trzy orbity paraboliczne o takich samych wartościach q)j. Każdorazowo testowano populację liczącą zaledwie 5000 komet.
W części dotyczącej zmiany odległości perihelium komety przed stawiono jedynie średnią zmianę q)j i jej odchylenie standardowe. Przedstawione w naszej pracy wyniki wskazują na bardzo silną za leżność zmiany q)j od geometrii przejścia gwiazdy co powoduje, że zamieszczone w pracy YHK wartości odchyleń standardowych są kilka lub kilkanaście razy większe od odpowiednich wartości średnich.
Przeprowadzone w pracy Schol i inni, 1982, rozważania jakościowe oparte są o równania wariacyjne Gaussa dla wielkiej półosi i mimośrodu. Zastosowanie tych równań do analizy zmiany orbity komety pod wpływem impulsowej zmiany prędkości nie daje prawidłowego obrazu, ponieważ nie opisują one przypadku skokowej zmiany wszystkich ( lub prawie wszystkich ) elementów orbity.
Zgodność bardzo ogólnych wniosków o znaku zmiany q)j z wynikami obliczeń w pracy SCB wynika znowu ze szczególnego doboru konfiguracji geometrycznych.

